Little 10 Toes
Master Poster
I think that doronshadmi's local/non-local is like Us vs. Them. If your not one of Us, then you're obviously one of Them. And each side thinks the same way.
I think that doronshadmi's local/non-local is like Us vs. Them. If your not one of Us, then you're obviously one of Them. And each side thinks the same way.
Well, except what has become painfully obvious is that his "us" is a singleton set.
The naïve notion is the false belief that there exists a complete non-finite collection such that distinct 0-dim elements totally covers a 1-dim element, or in other words, a 1-dim element is made of a complete collection of infinitely many distinct 0-dim elements.As your assertion is false so is your conclusion about the conclusion that your notions of set theory are simply naïve.
X vs. Y is a local-only reasoning, and by using this reasoning you can't get OM's reasoning, which is the linkage between Non-locality AND Locality under a one framework.I think that doronshadmi's local/non-local is like Us vs. Them. If your not one of Us, then you're obviously one of Them. And each side thinks the same way.
The "painfully obvious" is a direct result of your local-only reasoning.Well, except what has become painfully obvious is that his "us" is a singleton set.
The misrepresentation of my post is the basis of your post.Gibberish.
No, cardinality has nothing to do with names, unique or otherwise.
If you are trying to reference the Axiom Schema of Restricted Comprehension, then why not just say so?
...then you could avoid meaningless gibberish like this.
Be that as it may, since your misrepresentation of the axiom was the basis for the rest of your post, everything that followed is rendered meaningless. Try again.
The naïve notion is the false belief that there exists a complete non-finite collection such that distinct 0-dim elements totally covers a 1-dim element, or in other words, a 1-dim element is made of a complete collection of infinitely many distinct 0-dim elements.
Some example (both for closed or opened intervals):
Since accurate locations along a line (1-dim element) are determined only by points (0-dim elements) then each “9” of the expression “0.999...[base 10]” has an accurate location along the real-line.
If we take any arbitrary “9” location and look to the left of “0.999...[base 10]” expression we get finitely many “9” locations.
If we take any arbitrary “9” location and look to the right of “0.999...[base 10]” expression we get infinitely many “9” locations, such that no “9” location is exactly on the “1.000...” location.
As a result 0.999... < 1.000... exactly by 0.000...1, where “...1” of 0.000...1 is the invariant room that enables the existence of infinitely many “9” accurate locations to the right, which no one of them is located on 1.000... location.
If it was the case ( that 0.999... = 1.000...) then we had a finite amount of accurate locations from 1.000... to the left, which contradicts the existence of infinitely “9” along the “0.999...” expression.
Real analysis (standard or not) is based on a fundamental misunderstanding of infinity, because it can’t distinguish between actual infinity, which is not less than the total connectivity of a 1-D element , where any collection is a potential infinity w.r.t total connectivity, where total connectivity is not less then a non-local ur-element http://en.wikipedia.org/wiki/Urelement (represented by "...1" of "0.000...1" expression).
The misrepresentation of my post is the basis of your post.
Your local-only viewpoint of OM.What misrepresentation would that be?
Real analysis (standard or not) is based on a fundamental misunderstanding of infinity, because it can’t distinguish between actual infinity, which is not less than the total connectivity of a 1-D element , where any collection is a potential infinity w.r.t total connectivity, where total connectivity is not less then a non-local ur-element http://en.wikipedia.org/wiki/Urelement (represented by "...1" of "0.000...1" expression).
You do not have to. All you need is to understand ur-element as an element that belongs to some set but it is not itself a set.Funny, I don't see any mention of 'local' or 'non-local' elements on that page.
You do not have to. All you need is to understand ur-element as an element that belongs to some set but it is not itself a set.
It is very simple. What you do not undestend exactly?As someone before so eloquently put it: word salad.
OK, so if real analysis is based on a misunderstanding, how come it works? How come you can't show anything based on your "theory" that works?
Let's see... 1 is a number that belongs to the set of odd numbers but is not a set itself... Tough one to understand. What's your point? Also, why are you evading my questions?
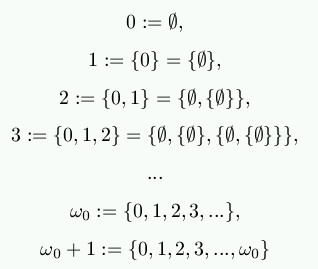
What do you mean?Please show something independent that uses OM.
If you believe that to be false then prove it by showing the location of any such gap. Otherwise continuing to claim what you cannot demonstrate , as well as yourself noting that such a location is “unknown” simply demonstrates that your notions and presentation and in fact naïve.The naïve notion is the false belief that there exists a complete non-finite collection such that distinct 0-dim elements totally covers a 1-dim element, or in other words, a 1-dim element is made of a complete collection of infinitely many distinct 0-dim elements.
Some example (both for closed or opened intervals):
Since accurate locations along a line (1-dim element) are determined only by points (0-dim elements) then each “9” of the expression “0.999...[base 10]” has an accurate location along the real-line.
If we take any arbitrary “9” location and look to the left of “0.999...[base 10]” expression we get finitely many “9” locations.
If we take any arbitrary “9” location and look to the right of “0.999...[base 10]” expression we get infinitely many “9” locations, such that no “9” location is exactly on the “1.000...” location.
As a result 0.999... < 1.000... exactly by 0.000...1, where “...1” of 0.000...1 is the invariant room that enables the existence of infinitely many “9” accurate locations to the right, which no one of them is located on 1.000... location.
If it was the case ( that 0.999... = 1.000...) then we had a finite amount of accurate locations from 1.000... to the left, which contradicts the existence of infinitely “9” along the “0.999...” expression.
Requirements
In the sense of this article, a naive theory is a non-formalized theory, that is, a theory that uses a natural language to describe sets. The words and, or, if ... then, not, for some, for every are not subject to rigorous definition.
Real analysis (standard or not) is based on a fundamental misunderstanding of infinity, because it can’t distinguish between actual infinity, which is not less than the total connectivity of a 1-D element , where any collection is a potential infinity w.r.t total connectivity, where total connectivity is not less then a non-local ur-element http://en.wikipedia.org/wiki/Urelement (represented by "...1" of "0.000...1" expression).
Poor The Man, you are like a person the wishes to see darkness by aiming a flashlight on it.If you believe that to be false then prove it by showing the location of any such gap. Otherwise continuing to claim what you cannot demonstrate , as well as yourself noting that such a location is “unknown” simply demonstrates that your notions and presentation and in fact naïve.
Just a hint, an “example” “both for closed or opened intervals” should actually involve at least some, well, intervals in that “example”
Once again simply demonstrating that your notions about set theory are naïve. In case you missed the imbedded link I gave before I’ll give it again, directly.
http://en.wikipedia.org/wiki/Naive_set_theory
Your reliance on vague and ill defined (often undefined) references intended to form your own natural language of OM like “the invariant room” and “enables the existence” simply confirms the fact that OM is intended to be “a naive theory”
So far your are the only one relying on fundamental misunderstandings and as a result there is absolutely nothing in your purported “analysis” that could even remotely be considered “real”. Again self-contradiction remains the fundamental misunderstanding of your notions. As given by your above example “Since accurate locations along a line (1-dim element) are determined only by points (0-dim elements)” then your “non-local ur-element http://en.wikipedia.org/wiki/Urelement (represented by "...1" of "0.000...1" expression)” is an ‘accurate location’ and entirely local by your own ascriptions. The fact that OM fails simply when applied to itself is all one needs to demonstrate your notions are entirely self contradictory as well as simply naïve.
It is very simple. What you do not undestend exactly?
Real analysis works in the physical world, if it translated to finite results.
OM deals with the difference and linkage between actual infinity (non-locality) and potential infinity of collections of localities that can’t be non-locality.
As a result we get a non-entropic space that can be useful for the survival of complex systems like us.
For better understanding of this subject, please look at:
http://www.internationalskeptics.com/forums/showpost.php?p=5008114&postcount=5726
