Myriad: "The relations might be linear in a strict technical sense, but they are not proportional as you appear to be implying, because of the sine and cosine functions of the tilt angle."
Incorrect. If we establish linearity in all 3 quantities a-b. b-r and r-98, the fact that they are directly proportional is obvious.
Anyone familiar with a Taylor Series? A Mclauren series?
Under small angle approzinmation, a sinusoidal wave can be written as an expanded Taylor series about any point, dropping the second order term and above.. If the point is the origin, this series is callesd a Mclauren series. It is pretty standard practice in physics.
In fact, have you ever tries to solve a 1 degree of freedom equation of motion for a simple pendulum? You will not be able to do that so easily without small angle approximation. If you just write out the
F =m
a fprm for a simple pendulum and try to solve for theta, you will see exactly what I mean.
You approximate sin(theta)=theta for small angles to solve it.
There are many things in physics which would be much messier without Taylor series expansion.
Myriad: "As I showed, the actual drop of the antenna base at one degree of tilt would be expected, for a rigid block, to be about forty times the actual drop of the north wall, which is less than half an inch."
The model shows you what is really expected. Your equations have no meaning if they deviate from that.
Myriad: "Half an inch, in reality. About seven "apparent" inches in the video."
"Apparent" inches, the drop as it appears from the Sauret perspective is exactly what we want.
Myriad: "About one, subject to the usual qualifier that "failure" is not (still not) a precisely defined enough event to specify a point in time with the necessary fraction of a second precision."
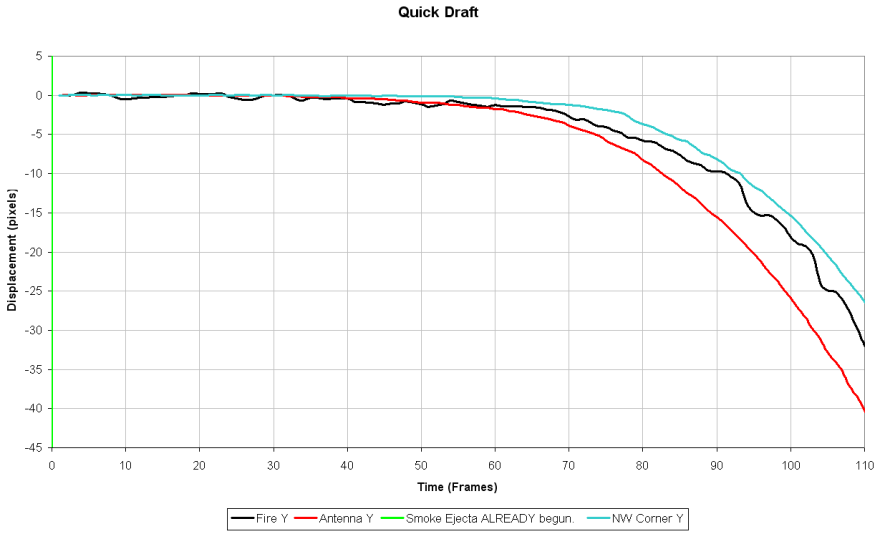
Incorrect. Spotting the obvious transition point when downward acceleration quicly changes from about zero to 0.5 to 1.0 g is another job that Koko can do.
Do you remember in another thread when TFK posted this silly graphic of a step function?
Original post here:
http://www.internationalskeptics.com/forums/showpost.php?p=6448912&postcount=550
With TFK's step function, can you spot the moment of failure? Koko can be taught to do it, no? Well, using the position and velocity drop curve for the NW corner the moment of failure is just about as obvious.
The transition moment is so obvious I don't know why you keep repeating this.
Myriad: "Yes, I know, you will now insist that NIST's scenario is utterly dependent on eight degrees of tilt before failure, and "prove" this by showing a graphic by R. Mackey that was intended to illustrate a completely different point, does not show an intact hinge, and does show two floors passing through each other. Go for it, maybe it will be more convincing on the 5th repetition."
No, I will make a model consistent with all observables just like I did with the OOS propagation model.
8 degrees is your problem, not mine. It comes up so much because many of you are in denail that
you have no collapse initiation model, not even an accurate description.
When we compare my model and yours (NIST's), this will become clear.
Myriad: "Yes I did read them, and no, not everything you think is in the links is actually there. But I was pleased to find that the math on the relations page is as close to correct as it is, though unnecessarily cryptic."
But you didn't understand it if you are still talking about non-linearity in the first 3 degrees of drop. Show me the parts you felt were unnecessarily complicated, and I'll consider rewriting them.
Myriad: "Perspective moderates this difference somewhat for the apparent drop, but even by the calculations in your own links, the apparent antenna drop is at least five times the apparent roof line drop."
Irrelevent. The hardest drop to detect is the NW corner, and the model rotating clearly shows that even 1 degree tilt is clearly visible and detectable.
WD Clinger post 640: "False. Your line r is the roof line, not the base of the antenna. As Myriad's simplified calculations demonstrate, the base of the antenna drops much faster than the roof line. That's why b-r decreases much faster than a-b or r-98."
Obviously. The proportionality constant is not 1. Differential relations between a-b, b-r and r-98 from 0 to 3 degrees here:
Large:
http://img541.imageshack.us/img541/7176/calmesant.png
Obviously b-r decreases much faster. the constants are given in the link in my last post.
Let's look at a-b compared to b-r:
The point is they are not moving together. It is the relationship between their slopes and curvature. They must slope and curve together to be parts of the same rigid body. As I wrote in the link:
a-b plotted in blue
b-r in pink on the right.
The constraint relations for a rigid body can be rewritten as
d(a-b)/df = c*d(b-r)/df where f is frame and c is a constant. This means the slopes of the blue and yellow lines must remain proportional to one another
and
second derivative of a-b w.r.t. f must equal c* second derivative of b-r w.r.t. f.
Simply stated, it means the curvatures of the two plots must remain proportional to one another.
(just think of f as a variable. Same equations if you use time t.)
>>>>>>>>>>>>>>> the 2 rigid constraints require that:
1) slopes of the two plots must remain fixed to each other (must remain directly proportional)
2) Curvature of the 2 plots must remain fixed to each other (must remain directly proportional)
If the blue and pink curves show rigid motion they have to slope together, curve together, move together, start to fall together.... basically do everything together.
Our two plots obviously, obviously do not move together. They are doing two totally different things. The only common feature between the two plots is they both eventually fall.
When the shapes of the plots of a-b and b-r don't share the same slopes or curvatures the antenna must be moving separately than the perimeter. They cannot be fixed together.
The different shapes of the blue and pink curves is in itself proof of deformity.
I also offered other ways to see roof-line deformity at the link. Did you read them?
WD Clinger: "Myriad didn't say his assumption was perfectly accurate. His assumption was close enough to demonstrate several problems with your approach, including your claim above of a linear relationship between three differences."
Incorrect. I know you are smart enough to expand the sine wave into a Taylor series over a small angle approximation. What are the first 2 terms in a Taylor series? (It's a line) The third term? (curvature)
If you work over a theta domain which is very small you can drop all terms above the linear. Try solving the pendulum problem without that assumption. Pretty standard trick in physics.
WDC: "Major_Tom's claimed linear relationship between a-b, b-r and r-98 is based on his implicit false assumption that the antenna is in line with the wall. "
Incorrect. It is based on small angle approximation.