Escape velocity from Earth is 11.2 km/s. A spacecraft leaving the gravitational field of the moon and falling on the Earth accelerates to a speed of 11 km/s before reaching the atmosphere at an altitude of around 120 km (see: Atmospheric entry). The kinetic energy corresponding to 11 km/s is around 60 Mega-Joule for every kilogram of spacecraft and crew. For comparison: energy content of jet fuel, gasoline and diesel is only around 45 MJ per kg (source).
Figure 4.1.7-25 of Returning from Space: Re-entry shows "Re-entry Profiles for the Shuttle Versus Gemini and Apollo":
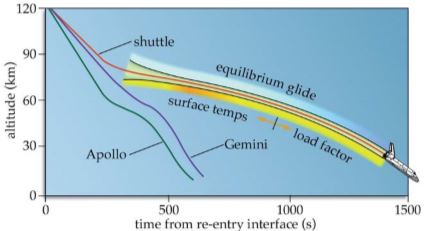
"Notice Gemini and Apollo re-entered much more steeply than the Space Shuttle."
According to this figure, Apollo needed around 250 sec to descent from altitude 120 km to 60 km. This results in an average speed of v = 60 km / 250 s = 240 m/s. To a speed of 240 m/s correspond only 28 kilo-Joule per kg, which is a negligible quantity in comparison to the 60 Mega-Joule corresponding to the entry speed of 11 km/s. Thus in the order of 99.9% of the kinetic energy must have disappeared before falling to an altitude of 120 km. Yet friction due to atmospheric pressure above 120 km altitude is too weak to relevantly reduce speed.
Wikipedia on meteors:
The return capsule of Stardust (bringing down to Earth dust samples in 2006) reached its maximum deceleration of 34 g (!) at an altitude of only 55 km:
So the question becomes even more acute: How could Apollo reduce its speed from 11 km/s to less than 1 km/s before or when entering the atmosphere (at an altitude of around 120 km)?
Cheers, Wolfgang
www.pandualism.com
Figure 4.1.7-25 of Returning from Space: Re-entry shows "Re-entry Profiles for the Shuttle Versus Gemini and Apollo":
"Notice Gemini and Apollo re-entered much more steeply than the Space Shuttle."
According to this figure, Apollo needed around 250 sec to descent from altitude 120 km to 60 km. This results in an average speed of v = 60 km / 250 s = 240 m/s. To a speed of 240 m/s correspond only 28 kilo-Joule per kg, which is a negligible quantity in comparison to the 60 Mega-Joule corresponding to the entry speed of 11 km/s. Thus in the order of 99.9% of the kinetic energy must have disappeared before falling to an altitude of 120 km. Yet friction due to atmospheric pressure above 120 km altitude is too weak to relevantly reduce speed.
Wikipedia on meteors:
"Meteors become visible between about 75 to 120 km above the Earth. They usually disintegrate at altitudes of 50 to 95 km."
The return capsule of Stardust (bringing down to Earth dust samples in 2006) reached its maximum deceleration of 34 g (!) at an altitude of only 55 km:
"On January 15, 2006, at 05:57:00 UTC, the Sample Return Capsule successfully separated from Stardust and re-entered the Earth's atmosphere at 09:57:00 UTC, at a velocity of 12.9 km/s, the fastest reentry speed into Earth's atmosphere ever achieved by a man-made object. The capsule followed a drastic reentry profile, going from a velocity of Mach 36 to subsonic speed within 110 seconds. Peak deceleration was 34 g, encountered 40 seconds into the reentry at an altitude of 55 km over Spring Creek, Nevada."
So the question becomes even more acute: How could Apollo reduce its speed from 11 km/s to less than 1 km/s before or when entering the atmosphere (at an altitude of around 120 km)?
Cheers, Wolfgang
www.pandualism.com


