Toontown
Philosopher
- Joined
- Jun 9, 2010
- Messages
- 6,595
What I really keep insisting on is that we don't have any evidence for an infinite universe. Or for a toroidal universe. The flat finite universe is what you're left with, but it doesn't seem to feature in contemporary cosmology.
Given nothing except GR as a guide, a perfectly flat universe is exceedingly unlikely.
GR says the geometry of space is determined by the mass density. There is 1 unique mass density that results in a perfectly flat universe. A razor edge. A myriad of other possibilities would appear flat unless the method of measurement is flawless.
The confidence level of the current flatness measurement is +/- 0.4%
If he'd given a coherent explanation that made physics sense, I'd be only too happy to accept it. He didn't, he just gave abstraction with no connection to reality that I could see. Could you?
Not sure. If I'm visualizing it right, I suppose a flat triangle might be drawn on a doughnut-shaped surface. "Flat" in the sense that the internal angles sum to 180*.
But I'm not a fan of a toroidal universe. There is no data that calls for it.
I don't like it because my understanding of relativity makes me think that a homogeneous universe is a flat universe. That's what the FLRW metric starts with, and in that universe (setting expansion aside) light goes straight.
My understanding of GR is that the mass density determines the curvature.
And "straight" is relative to the geometry of the space it's moving through, being the shortest path through the space.
It doesn't alter its nature, it just ends. Waves can't propagate beyond it. So I speculate that they'll undergo total internal reflection.
Reflect off of what? Nothing?
I think you've just invented a new something. A something called nothing. And that's been the problem with edged space all along.
I don't think it is. The universe is thought to have started as something small and dense, even a "singularity".
If the universe is infinite, then it was never "small". Dense I'll grant, but never small. Just tightly packed.
I'm not keen on singularities myself, but nevermind.
A "singularity" is not necessarily a point, though it could be. "Singularity" means oneness - a singular entity. Size doesn't define what "singularity" means. A singularity can be infinite in size, as long as it's a singular entity - a oneness.
With a finite age of 13.8 billion years, it just can't be infinite. I see no method by which it can be some kind of "Asteroids" universe. So I'm left with finite space beyond which there is no space, so there is no beyond it.
Sure, if you keep insisting that it started as a point singularity, in which case I suppose, given current observations, you need infinite expansion velocity or a replacement for GR.
But the truth is, IF the universe is infinite, and if GR holds, then the universe did NOT begin as a point singularity - unless something wierd beyond my comprehension happened. A singularity, perhaps, in the "oneness" sense, but not a point. Meaning, in essence, that what changed was it's density, not it's size. And it transformed from oneness to a multiplicity of things.
The "point singularity" was a speculation, not a necessity.
Nice track.
Half the Beatles were in it.



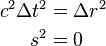

 .
. !
!.gif) :
: