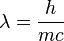Merged Relativity+ / Farsight

[Reality Check]

What value is that edd? The fine structure constant? I tell you, that varies with gravitational potential, and there's gravitational fields everywhere.

Farsight, we can tell that you are even unable to look up the fine structure constant in Wikipedia!

In physics, the fine-structure constant (usually denoted α, the small Greek letter alpha) is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction.

It depends on:

where:

• e is the elementary charge;
• ħ = h/2π is the reduced Planck constant;
• c is the speed of light in vacuum;
• ε0 is the electric constant or permittivity of free space;
  • or µ0 is the magnetic constant or permeability of free space;
  • or ke is the Coulomb constant.

None of these constants depends on a gravitational field.
I will preempt any rant about the speed of light varying in a gravitational field, Farsight. The speed of light above is the constant speed of light that appears ion GR. It is not the coordinate speed of light that varies according to whatever coordinate system an observer arbitrarily picks to use.

 

[Reality Check]

And it's world-class wrong.
...snipped a rant about basic facts (electrons have wavelengths! So do protons and C60 and even baseballs ! That is basic QM)...

And by stating this without seemingly even looking at the paper you go beyond world-class wrong into the realm of the ultimate crackpot .
A Combination of Preliminary Electroweak Measurements and Constraints on the Standard Model (2006)

This note presents a combination of published and preliminary electroweak results from the four LEP collaborations ALEPH, DELPHI, L3 and OPAL based on electron-positron collision data taken at centre-of-mass energies above the Z-pole, $130 \GeV$ to $209 \GeV$ (\LEPII), as prepared for the 2006 summer conferences. Averages are derived for di-fermion cross sections and forward-backward asymmetries, photon-pair, W-pair, Z-pair, single-W and single-Z cross sections, electroweak gauge boson couplings, W mass and width and W decay branching ratios. An investigation of the interference of photon and Z-boson exchange is presented, and colour reconnection and Bose-Einstein correlation analyses in W-pair production are combined. The main changes with respect to the experimental results presented in 2005 are new preliminary combinations of final {\LEPII} results on the mass and width of the W boson. Including the precision electroweak measurements performed at the Z pole published recently, the results are compared with precise electroweak measurements from other experiments, notably CDF and D{\O}at the Tevatron. Constraints on the input parameters of the Standard Model are derived from the results obtained in high-$Q^2$ interactions, and used to predict results in low-$Q^2$ experiments, such as atomic parity violation, M{\"o}ller scattering, and neutrino-nucleon scattering

This is a review that includes actual measurements of the size of the electron and restricts the electron radius to less than 1.4 × 10−19m from scattering experiments.
Studies of single electrons in Penning traps provide a more restrictive (but more theoretical!) upper limit of less than 10⁻²²m.
A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius

From the close agreement of experimental and theoretical g-values a new, 104 × smaller, value for the electron radius, Rg < 10-20 cm, may be extracted.

 

[Reality Check]

Farsight: Just what did you nail in "Reality check at the LHC"?

Wow - I really should not look back in Farsight's threads because I find so many unanswered questions !

Farsight: Just what did you nail in "Reality check at the LHC"?
First asked 20th April 2012.
Farsight, does Relativity+ predict that the Higgs boson does not exist?
First asked 23rd April 2012.

Farsight has not been able to learn physics for oh so long, e.g. the definition of the fine structure constant which he still thinks depends on gravity!

That it reduces with gravitational potential.

To which I pointed out what he still is in denial of:

Note the absence of any gravitational constants like G.
P.S. In case you go about the speed of light varying: c is a constant and the coordinate speed of light means that a set of coordinates can be picked where the fine structure constant is as close to zero as you want (in fact any value).

Farsight is still going on with the fallacy of argument from authority even when the authorities he cites say that he is wrong, e.g. Maxwell is quite happy with there being electric, magnetic and electromagnetic fields.
W.D.Clinger pointed out Farsight's ignorance of Einstein and thus GR back on 28th April 2012. Nothing seems to have changed.

The answer to Farsight: Do you understand the fallacy of argument by authority? asked on 27th March 2012 is still seems no !

 

[Tim Thompson]

Electric & Magnetic Fields

So many posts, and such spread out & confused issues. So let me pose the obvious question to Farsight, maybe already answered somewhere buried in some thread, but clear explicit statements seem hard to come by: Do you claim that the electric field is not in fact a "field" at all, and that it is wrong to call it a "field", given some appropriately rigorous definition for a "field"?

I asked because the issue of what Farsight really means seems to be clouded by Farsight's own words, for example …

On 19 June ...

I said the electromagnetic field is a field, but that the electric field and the magnetic field aren't.

On 21 June ...

Yes it can be useful to talk of electric fields and magnetic fields separately, ...

The first is certainly a clear enough claim that the electric and magnetic fields are not in fact fields. But then only two days later, he implies that, OK, they are fields and it may even be useful to talk about them, but it's really the electromagnetic field we should always be talking about. I am not going to worry about mind-reading at the moment, and just look at the two points, as I see them.

First the easy one, the idea that electric & magnetic fields are useful, but it's really the electromagnetic field we should be talking about. Well, really, everybody who ever studied physics (and remained awake in class at least most of the time) knows very well that Maxwell took electric and magnetic and created from them the unified electromagnetism. And physicists certainly do talk about the unified electromagnetic field whenever it is appropriate, and likewise about electric and magnetic fields when they are appropriate; as Farsight suggests, it is useful, but apparently more useful than he thinks. Allow me at this point to shamelessly quote from the collected literature of physics:

"The force of the first type, per unit charge, is called the electric field intensity; we denote it by E. So, by definition,

E = -(1/c)(∂A/∂t) - grad Φ

The factor of v/c in the force of the second type, per unit charge, is called the magnetic field intensity. We designate it by H. So, by definition,

H = curl A

[highlight]If, in an electromagnetic field, E ≠ 0 but H = 0, then we speak of an electric field; if E = 0 but H ≠ 0, then the field is said to be magnetic. In general, the electromagnetic field is a superposition of electric and magnetic fields.[/highlight]"

The Classical Theory of Fields (4th revised English edition), Landau & Lifshitz , 1975 (reprinted with corrections 2005). Chapter 3, "Charges in Electromagnetic Fields" (pages 50-51, italics from the original; the highlight is mine).

Two for the price of one. Clearly, if electro = nothing but magneto = something, then we don't have electromagnetism, we just have magnetism, and vice-versa. But we also see that the electric field and the magnetic field combine into the electromagnetic field; there is nothing about the physics of fields which prevents one field from being a superposition of multiple other fields. In this case the two, electric & magnetic, combine into the third, electromagnetic. The idea that electric fields and magnetic fields are not fields, as explicitly pointed out at least once by Farsight, does not seem to pass the test of physics (as most of you of course already know).

Now, about that "what is a field" thing. Since my own brief & casual foray into trying to find a reasonably rigorous definition for a "field" was unsatisfactory, let me try again, after following the advice to "do my own research".

A field is a function that associates one or more numbers with each point in space. Two types of field are distinguished: scalar and vector, depending on whether the field function assigns either a scalar or a vector value to each spatial location. The gravitational potential of the Earth is a scalar field, and the force of gravity is a vector field (all forces point towards the center of the Earth).
The Six Core Theories of Modern Physics, Charles F. Stevens, MIT Press 1995 (sixth printing, 2002), page 2 (emphasis from the original).

I was rather hoping for something that combined brevity with rigor; while this seems to award the former more than the latter, it still seems both rigorous enough & correct enough for our work. It should be, as my old instructors liked to say, "obvious by inspection" that both the electric field and the magnetic field meet the criteria established here for a field (the definition does not deal with the technicality of vector vs pseudovector, in describing a vector field, but if one allows a casual use of the word "vector" it does the job).

But maybe we can do better ...

"The interaction of particles can be described with the help of the concept of a field of force. Namely, instead of saying that one particle interacts with another, we may say that the particle creates a field around itself; a certain force then acts on every other particle located in this field. In classical mechanics, the field is merely a mode of description of the physical phenomenon - the interaction of the particles. In the theory of relativity, because of the finite velocity of propagation of interactions, the situation is changed fundamentally. The forces acting on a particle at a given moment are not determined by the position at that same moment. A change in the position of one of the particles influences other particles only after the lapse of a certain time interval. This means that the field itself acquires physical reality. We cannot speak of a direct interaction of particles located at a distance from one another. Interactions can occur at any one moment only between neighboring points in space (contact interaction). Therefore we must speak of the interaction of the one particle with the field of the second particle."

The Classical Theory of Fields (4th revised English edition), Landau & Lifshitz , 1975 (reprinted with corrections 2005). This is the first paragraph of chapter 3 (page 46), "Charges in Electromagnetic Fields" (emphasis from the original).

I present that, so as to address this ...

Neither of those particles ever had an electric field as opposed to an electromagnetic field.

This strikes me as an issue of semantics, not physics; indeed, in any sense of physics, it's just absurd. As an exercise in semantics, it might be forgiven. Given the various definitions shown above, an electric field is an electromagnetic field with the magnetic component equal to zero. Choose either one, and it will work just fine. Then we can splutter on as long as we like that it must be an electromagnetic field, not an electric field, and have language available whereby to feel better about ourselves. But the physicist will ignore the linguistic mumbo-jumbo and simply treat the particle as having an electric field and be done with it.

Some windmills are useless tilting targets, and this is one. Of course the electric field and the magnetic field are real-live, honest to gosh fields, and all the linguistic tricks and clever exegesis of physics texts will not change that. Everything in physics is what the equations say it is, and if the equation says "field", then by golly it's a field, like it or not. And that is exactly what the equations say.

 

[Kwalish Kid]

But Farsight is getting beyond the equations to the real physics. The equations just confuse the issue, because the actual physical things are not equations but actual physical things.

Farsight, somehow, has a deep insight into the actual physical things without any of the mathematics. Somehow, he has to convince us of this deep insight and of his legitimacy in this area, without using any mathematics.

Wouldn't it be better evidence for the general theory of relativity to appeal to experiments and observations without any use of mathematics?

 

[Reality Check]

What are the units of" c½/3πn", Farsight

You know full well they're Andrew Worsley's quantum-harmonics expressions for 1) electron Compton wavelength

Without a citation to this person who has never been mentioned in this thread that "know full well" is a delusion, Farsight .

Electron Compton wavelength is defined with as:

The Compton wavelength, λ, of a particle is given by

where h is the Planck constant, m is the particle's rest mass, and c is the speed of light.

This is not "4πn/√(c³)", so you are wrong.
So the rest of your post based on this is just gibberish.

So who is Andrew Worsley?
There is Andrew Worsley (2011) Harmonic quintessence and the derivation of the charge and mass of the electron and the proton and quark masses. Physics Essays: June 2011, Vol. 24, No. 2, pp. 240-253.
He claims to have a ground-breaking new theory (harmonic quintessence) that explains the origin of mass. There are indicators that he is a crank though

• This amazing theory is published in an obscure journal behind a pay wall.
• His theory starts with the equation E = hn where E is energy h is Planck's constant and n is a number.
  This is not harmonic nor quintessence !
• That n presumably is the n that appears in the above equation.
  If that is right then Andrew Worsley is really dumb because he has got the units of measurement wrong.

2) the electron-proton mass ratio{/quote]
Oh dear - this is something even you should now is wrong", Farsight !

A ratio has no units. What are the units of" c½/3πn", Farsight?

Because the electron is a point-particle dear boy, one that gets its mass from cosmic treacle, and can be in two places at once. Whoa! Multiverse!

Whoa! Ignorance, Farsight !
It is QM and experiments that show that an electron can be in "two places at once", e.g. electrons going one by one through a two slits can "self interfere" (act as if they went through both).

 

[edd]

I've spoken about non-constant constants enough times. But there you are peddling the Goldilocks multiverse. Because you like woo. So much so that when I try to explain something and present the evidence, you dismiss it. The fine-structure constant α=e²/2εchc isn't constant, Planck's constant might not be, and optical clocks run slower when they're lower. You know that the same will be true for parallel-mirror light clocks, and you know that the coordinate speed of light varies in a non-inertial reference frame. So you know c is merely defined to be constant. You also know about conservation of charge and you know that c=√(1/εₒμₒ). So you ought to be able to look at α=e²/2εₒhc and ask yourself what's actually changing here? And since the Planck mission has found large-scale inhomogeneities, that might mean Lambda isn't constant either. But that's OK, you can happily dismiss all this as bluster, arrogance, and ignorance. Don't let mere physics get in the way of your precious multiverse, eh?

Since Farsight has resurrected these claims yet again in the thread L. Susskind -- The "Megaverse", I thought I'd encourage him to back up his claims here.

Farsight seems to think that because the fine structure constant changes at high energies that this might explain possible 'fine tunings' in the universe. So...
1) Can you, Farsight, explain how life here at a typical temperature of say 300K could as a result of running constants experience a different fine structure constant to life in some other part of the universe, also at a typical temperature of around 300K?
2) Can you estimate the order of magnitude of the difference in fine structure constant found by some rather implausible alien thermophilic life existing at, say, 3,000K instead of 300K?
3) Take an extreme astrophysical energy that may be considered to play a role in the development of life - lets take the temperature at the core of a supernova about to go off and spread all those heavy elements that life can find useful out into space - call it 3,000,000,000K. Estimate the order of magnitude difference in fine structure constant in that case.
4) Reverse the problem. Suggest very roughly at what temperature would one measure a fine structure constant of, say, 1/135 instead of 1/137. Describe what chemistry looks like at that sort of temperature and what kind of life might arise in those conditions*.

I'll give you a bit of helpful information: the measurements of the running typically involve experiments operating at GeV scales.

So you ought to be able to look at α=e²/2εₒhc and ask yourself what's actually changing here?

Incidentally I think there are subtleties here that are easily missed. http://arxiv.org/abs/hep-th/0208093 is a useful read.


*those following along at home may notice that this could be considered something of a trick question

 

[Perpetual Student]

Since Farsight has resurrected these claims yet again in the thread L. Susskind -- The "Megaverse", I thought I'd encourage him to back up his claims here.

Farsight seems to think that because the fine structure constant changes at high energies that this might explain possible 'fine tunings' in the universe. So...
1) Can you, Farsight, explain how life here at a typical temperature of say 300K could as a result of running constants experience a different fine structure constant to life in some other part of the universe, also at a typical temperature of around 300K?
2) Can you estimate the order of magnitude of the difference in fine structure constant found by some rather implausible alien thermophilic life existing at, say, 3,000K instead of 300K?
3) Take an extreme astrophysical energy that may be considered to play a role in the development of life - lets take the temperature at the core of a supernova about to go off and spread all those heavy elements that life can find useful out into space - call it 3,000,000,000K. Estimate the order of magnitude difference in fine structure constant in that case.
4) Reverse the problem. Suggest very roughly at what temperature would one measure a fine structure constant of, say, 1/135 instead of 1/137. Describe what chemistry looks like at that sort of temperature and what kind of life might arise in those conditions*.

I'll give you a bit of helpful information: the measurements of the running typically involve experiments operating at GeV scales.


Incidentally I think there are subtleties here that are easily missed. http://arxiv.org/abs/hep-th/0208093 is a useful read.


*those following along at home may notice that this could be considered something of a trick question

 

[Farsight]

It does not appear obvious to me that anyone on this board assumes or accepts there is a multiverse. Everyone here seems to regard it as speculation

I regard it as woo.

You now appreciate that the fine structure constant isn't constant. OK?

So why presume that the cosmological constant is constant? See wiki, Λ is equivalent to an energy density in otherwise empty space. But space isn't empty, energy density varies with gravitational potential, there's gravitational fields everywhere. In addition the universe is expanding over time and conservation of energy is one of the most important tenets in physics. And people can't actually find any cold dark matter particles. But energy does have a mass equivalence. Even when it's the energy of space alone.

IMHO the ΛCDM model will end up as the variable-Λ model, and the Goldilocks multiverse will be remembered with ridicule on a par with the flat Earth and phlogiston.

 

[edd]

So why presume that the cosmological constant is constant?

Umm we don't. We assume it until we have evidence otherwise, and we (yes including me in very small ways) are working on experiments to try to show it doesn't.

I must now trawl the forum to see if you dealt with my challenges to your claims about the fine structure constant variation and its relevance to anthropic arguments.

Edit to add: nope. Here you go Farsight - http://www.internationalskeptics.com/forums/showpost.php?p=9336221&postcount=987

 

[Reality Check]

I regard it as woo.

Well, Farsight, I regard it as a valid scientific theory with little evidence supporting it. For some strange reason that is what it is in the real world !

Everyone knows that the fine structure constant is a variable by definition but not by name. This is a historical accident because it was defined decades before the formation of QFT and the discovery that it would vary with energy.

This has nothing to do with the cosmological constant which is defined as constant and named as a constant.

Try reading what you cite from wiki, Farsight:

In cosmology, the cosmological constant (usually denoted by the Greek capital letter lambda: Λ) is equivalent to an energy density in otherwise empty space.
...
The cosmological constant has the same effect as an intrinsic energy density of the vacuum, ρvac (and an associated pressure).

(my emphasis added)
IOW: Λ is equivalent to an energy density in an empty universe.
IOW: Λ is the cost of having space-time regardless of the contents of the universe.

In addition the universe is expanding over time and conservation of energy is one of the most important tenets in physics

Whatever do you mean by that, Farsight?

Both assertions are correct by themselves

• the universe is expanding over time
• conservation of energy is one of the most important tenets in physics

But they have nothing to do with each other.
FYI: The expansion of the universe does conserve energy.

And people can't actually find any cold dark matter particles.

And this is irrelevant for this thread.
There is lots of evidence that dark matter exists. There are plenty of candidates for what it could be. If dark matter is made of something that can be detected directly then it will be detected directly.

But energy does have a mass equivalence

Well Duh !

Even when it's the energy of space alone.

Wrong: You seem to not know the meaning of mass–energy equivalence

In physics, mass–energy equivalence is the concept that the mass of a body or system is a measure of its energy content. In particular, any physical system has a property called energy and a corresponding property called mass; the two properties are always present in the same (i.e. constant) proportion to one another. This means (for example) that the total internal energy E of a body at rest is equal to the product of its rest mass m and a suitable unit conversion factor which transforms units of mass to proportionate units of energy.

Space is not a "body or system" and does not have a rest mass! Think about it, Farsight - space is at rest with respect to what? More space? Space outside of space?

There is a trivial sense in which you are right - the universe is a system and we could consider all of it as energy and get a "rest mass".

In the real world the ΛCDM model will end up as the variable-Λ model if there is evidence that Λ varies, and this has nothing to do with the multiverse.
If there is evidence that there is no multiverse then the scientific theory of multiverse will be remembered with respect on a par with Newtonian mechanics and old quantum theory.

 

[Toontown]

Space is not a "body or system" and does not have a rest mass! Think about it, Farsight - space is at rest with respect to what? More space? Space outside of space?

Your beseeching is futile. Farsight also thinks space has an edge, and anything that hits the edge of space bounces off. That's gotta be some massive space. Hard, too.

No, it's not because there is space outside of space. The impenetrable edge prevents any space from leaking out into nothing. That's kind of why it has an edge. Also to keep flat space from being infinite. But that's another long story.

If there is evidence that there is no multiverse then the scientific theory of multiverse will be remembered with respect on a par with Newtonian mechanics and old quantum theory.

When Farsight is vindicated, everything that ever annoyed him will be remembered only with derision. That's his prediction, and darn it, he's good at those predictions.

 

[Vorpal]

No, it's not because there is space outside of space. The impenetrable edge prevents any space from leaking out into nothing. That's kind of why it has an edge. Also to keep flat space from being infinite. But that's another long story.

What? Why not just have it wrap it around instead?

 

[Toontown]

What? Why not just have it wrap it around instead?

Because it is observed to be flat or very nearly flat, which means infinite or very big if you don't do something. I suppose Farsight wanted to chop it off before it grew to level 1 multiverse size.

 

[Farsight]

Umm we don't. We assume it until we have evidence otherwise

We already have evidence in the guise of gravitational anomalies. Energy causes gravity, not just matter in the form of particles. We can't find any WIMPs, and Λ is equivalent to an energy density in otherwise empty space.

and we (yes including me in very small ways) are working on experiments to try to show it doesn't.

You will find that it does. The energy density of space varies in a gravitational field. A gravitational field is a place where the energy density of space is not uniform.

I must now trawl the forum to see if you dealt with my challenges to your claims about the fine structure constant variation and its relevance to anthropic arguments.

But you acknowledge that it varies. Good.

Edit to add: nope. Here you go Farsight - http://www.internationalskeptics.com/forums/showpost.php?p=9336221&postcount=987

Challenge? That's no challenge? Why are you asking about temperature when I said the fine structure constant varies with gravitational potential? That's a straw man, not a challenge. One that attempts to defend the fantasy of a Goldilocks multiverse.

 

[Farsight]

Well, Farsight, I regard it as a valid scientific theory with little evidence supporting it. For some strange reason that is what it is in the real world !

It's woo, just like heaven and hell and unicorns and fairies.

Everyone knows that the fine structure constant is a variable by definition but not by name. This is a historical accident because it was defined decades before the formation of QFT and the discovery that it would vary with energy.

Everybody here now knows it because I've been banging the drum about it.

This has nothing to do with the cosmological constant which is defined as constant and named as a constant.

Conservation of energy tells you it varies over time. Unless you believe in magick. I'm telling you it varies across space too.

Try reading what you cite from wiki, Farsight:

(my emphasis added)
IOW: Λ is equivalent to an energy density in an empty universe.
IOW: Λ is the cost of having space-time regardless of the contents of the universe.

Wikipedia is pretty good, but not always right. Spacetime is an abstract mathematical "space". The cosmological constant is equivalent to an energy density in otherwise empty space, not spacetime.

Whatever do you mean by that, Farsight?

Both assertions are correct by themselves

• the universe is expanding over time
• conservation of energy is one of the most important tenets in physics

But they have nothing to do with each other.
FYI: The expansion of the universe does conserve energy.

Then the energy density of otherwise empty space has to be reducing, doesn't it? Unless you believe in magick.

And this is irrelevant for this thread.
There is lots of evidence that dark matter exists. There are plenty of candidates for what it could be. If dark matter is made of something that can be detected directly then it will be detected directly.

Try detecting space.

Wrong: You seem to not know the meaning of mass–energy equivalence

Space is not a "body or system" and does not have a rest mass!

Bah, you know nothing. Einstein said the energy of a gravitational field shall act gravitatively in the same way as any other kind of energy. Wave your hand around in the space where a gravitational field is. Are there any WIMPs there? No. But this space has a higher than usual energy density, and that has a gravitational effect.

If there is evidence that there is no multiverse then the scientific theory of multiverse will be remembered with respect on a par with Newtonian mechanics and old quantum theory.

No it won't. It will be remembered as woo peddled by quacks lapped up by suckers.

 

[Farsight]

What? Why not just have it wrap it around instead?

The universe is "flat", and it's expanding. IMHO that means there's no higher-dimensional curvature and it can't be infinite. Ergo it has to have some kind of edge. The analogy is a droplet of water. A ripplet in the water can't go outside the water, and instead suffers total internal reflection. But it's a bit off topic, so maybe you'd like to start a thread on it.

 

[Farsight]

How is this true?

α = e²cμ₀/2h -- among several other expressions (LINK), all consisting of constants. So, how can α vary with energy? Does e vary with energy? How about μ, c or h? These are all constants that do not vary. If you can do so, please explain.

(Farsight: I really have no interest in Duffield-make-believe, so don't bother to respond. This thread is for people who have a genuine interest in physics and cosmology; there is a separate thread discussing crackpots.)

I'm not the crackpot here, the crackpots peddle Goldilocks multiverse woo. So I will respond, to shoot down that woo:

1) e does not vary. Conservation of charge applies.
2) μ, c or h do vary.

See http://physicsworld.com/cws/article/news/2012/mar/28/can-gps-find-variations-in-plancks-constant re possible variations in h. I'm not sure if it does vary myself, but I am utterly sure that μ and c do because the coordinate speed of light varies in a non-inertial reference frame such as gravitational field, and c = √(1/ε0μ0).

NB: the typical QED given explanation refers to virtual particles and "screening", and suggests that effective charge varies. But don't forget that virtual particles are virtual. They are field quanta, like you divide up the space where the field is into little squares. There are no actual particles popping in and out of existence. See Matt Strassler's article for more on virtual particles. The effect of the charge varies because the properties of space described via μ c and h vary. The charge doesn't.

 

[ctamblyn]

The idea that the type of variation of e/m coupling strength predicted by quantum field theory (the so-called running of the coupling constant alpha) is relevant to issues of fine tuning which are the theme of this thread is patently ridiculous. John Duffield has been challenged to calculate the actual variation in various scenarios, but is unable to back up his vague assertions at all with actual calculations (or is perhaps unwilling to do so, as it would immediately reveal the flaw in his argument).

 

[sol invictus]

I'm not the crackpot here, the crackpots peddle Goldilocks multiverse woo. So I will respond, to shoot down that woo:

1) e does not vary. Conservation of charge applies.
2) μ, c or h do vary.

Which piece of alpha varies is a matter of convention. Constants with dimensions can vary or not - it's entirely up to you and the units you choose. It's only variation in dimensionless combinations of constants (like alpha) that means something physically. But e is the most natural choice.

To say that e cannot vary because of conservation of charge is completely wrong. We're not talking about variations in alpha as a function of time (although even if we were, it would still be wrong).

The "running" of alpha in quantum field theory is as a function of energy scale. It occurs primarily because of virtual electron/anti-electron pairs. The vacuum is full of such pairs, and the more energy your probe has, the more of them it encounters. Charges in a solid or a plasma get screened - they attract opposite charges and repel like charges, which means the charge inside a sphere drawn around the charge is smaller than the "bare" value of the charge. The same happens with the vacuum in QFT - that's why alpha increases at high energy.