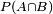At the risk of repeating myself.... (well, the whole thread is on a repeat cycle I suppose)
According to Wikipedia, the first publication of the puzzle dates back to 1975. (When did the Monty Hall TV show start, does anyone know?) The exact wording of that publication isn't stated, but going from CurtC's and Claus's insistence that the "Monty will always open one of the two unchosen doors and will always reveal a goat" version is The Only True Authentic Monty Hall Puzzle, I'm assuming that perhaps it did make this clear.
However, as far as I can see, the perennial fascination owes a great deal to the fact that subsequent wordings of the scenario have become more ambiguous. I can't see how a puzzle clearly and precisely defined as above could be anything more than a nine-day wonder.
Certainly, when I first encountered the puzzle in 1994 or thereabouts, the wording was similar to the OP, and arguably ambiguous. And then, as now, the bulk of the argumentation seemed to revolve around exactly what rule Monty is to be supposed to be working to. And to be honest, I think this raises the debate to a whole new level.
If we just consider what Claus and CurtC and others call the "classic Monty Hall" scenario, yes, it's intriguing, and counterintuitive, but the answer is perfectly clear once you've got your brain around it. I think it took me a day or two, just puzzling at it on my own, to get there. Really, really, even though there might be some dimwits who will never get it, there isn't a debate. Switching doubles your chances of getting the car, full stop. End of.
All everybody has been arguing about for most of this thread is interpretation. Exactly what game are we playing anyway?
I know how I got on to that aspect, and I think it's how many people have got there. I imagined the 100-doors version (99 goats and a car), while I was thinking about the basic puzzle. This illustrates how the odds change during the process, but it also clarifies the need to know what the exact rules are.
Contestant chooses a door. Monty opens another, a goat. Switch? Wouldn't make much difference, you've still got 98 other doors. But as the process is repeated and repeated, the situation becomes much clearer. The longer the car remains unrevealed, the clearer it becomes that Monty is deliberately avoiding it. By the time there are only two doors left, two things are obvious. The probability that Monty is deliberately avoiding the car is 98/100. And it should be completely intuitive that you should switch. Because the probability that the car is behind the door you originally chose is and always was 1/100, therefore the probability that it is behind the other door is 99/100.
For me, it was this exercise that clarified the need to stipulate the exact rules. Because in the 100-doors version, if Monty was opening doors at random, with no more idea than you have of where the car is, then in the overwhelming majority of games, he'd have revealed the car behind one of the other doors way before you're left with only two closed doors.
And once you think about it, that is also a reasonable interpretation of the wording of the puzzle as usually presented. And, indeed, a reasonable way of running a game show.
Contestant picks a door. Monty, who has no idea where the car is, opens one of the other two doors at random. A third of the time he reveals the car. Oh too bad sir, thanks for playing, good game, hope you and your goat will be very happy together. Two thirds of the time he reveals a goat. Well sir, so far so good, but would you like to change your choice? In that situation, switching makes bugger-all difference.
Cue argument that lasts for (to date) 33 years.
But then it gets worse. Now that the matter of the exact rules has been opened to scrutiny, people start getting even more creative. What if Monty is a complete bastard, and will only open the door if he knows you've already got the car? Well, unlike the random-opening scenario, that is neither a sensible game show, or a reasonable brain-teaser. As one of a range of possibilities incorporated in my next scenario (capricious Monty) it has a place. However, as a consistent stratagem, it's a nonsense. It's just a hypothetical scenario that is dragged in for the sake of argument.
But what if Monty is totally capricious? Maybe he'll help some contestants and be a bastard to others. Maybe he has a different scenario in his head every time the game is played! From what I've heard from those who have watched the original show, this may well have been the actual case. And presumably it was a perfectly viable game show.
However, it's not a perfectly viable brain teaser. To have any validity as an abstract puzzle, there has to be consistency. To put the question to anyone and then say, well, there's no right answer because Monty is entirely capricious, isn't a lot of fun.
For these reasons I maintain that it is reasonable to exclude both the "Monty-is-a-bastard" scenario and the "Monty-is-capricious" scenario. No game show could possibly persist if the former scenario was being operated, and no rational brain-teaser could employ the latter.
Nevertheless, what I will call the "B" scenario, the one where Monty doesn't know where the car is but simply opens one of the two doors the contestant hasn't chosen, is valid as a brain teaser and as a game show, and is in accordance with the usual, ambiguous, wording of the puzzle. (I'm designating the "real" Monty Hall puzzle, where he knows where the car is and will avoid opening that door at this stage, as the "A" scenario.)
This is the conundrum I find completely and utterly fascinating.
The puzzle is as presented. It is not clear whether the A or the B scenario is intended. (That is, you deduce that Monty opening one of the doors you didn't choose is a prerequisite, but you don't know whether or not he knows where the car is.) Where does that leave you?
It leaves you in the peculiar position where the correct answer depends entirely on what is going on in the mind of the host. And in my experience it is that very surreal situation that causes the most outcry from those who have difficulty with the puzzle.
I can only really get my brain round it by imagining that I'm playing one of two computer-game versions. One is programmed with the "A" version, and the other with the "B". I've got to the point where one of the doors I didn't choose has been opened, and there is a goat there, but I still don't know which one I'm playing. If it's the "A" version, I know that switching will double my chances of winning, but if it's the "B" version, I know that switching won't make a blind bit of difference.
Seems sensible enough when looked at that way.
However, I'm not playing with computers. There is an actual person there. Monty just opened a door to reveal a goat. Will switching improve my chances of winning? Well, the answer depends entirely on whether or not Monty himself knows where the car is.
Surreal, what?
Rolfe.