When some observed time series is approximated over an interval (t0, t1) by some polynomial P of excessively high degree, then the derivative of P is more likely to have large absolute value near the endpoints t0 and t1 than if a polynomial of lower degree had been used. That, in turn, makes it more likely that P(t) will be a poor approximation to the time series at times t that are just outside the interval.
I suspect that's why femr2's Poly(10) model is so inaccurate between 11 and 13 seconds
I suspect you are being hampered by what I would call
chosen field hubris.
I am finding it harder and harder to believe that you cannot see the straightforward nature of what I'm placing in front of you.
At the911forum this would be a
HTFCYNST moment.
Consider...
http://femr2.ucoz.com/_ph/7/513801604.png
- The Savitzky-Golay smoothed profile does not suffer from large absolute value near the endpoints t0 and t1. It shows the true trend of acceleration of the NW corner over time, and in considerable detail as far as I'm concerned.
- Both the Poly(10) and Poly(50) profiles correlate exceedingly well with the S-G profile.
- The same general profile trend emerges whatever methods have been chosen to transform from displacement/time to acceleration/time, whether it is myself or someone else, such as tfk, doing the leg-work.
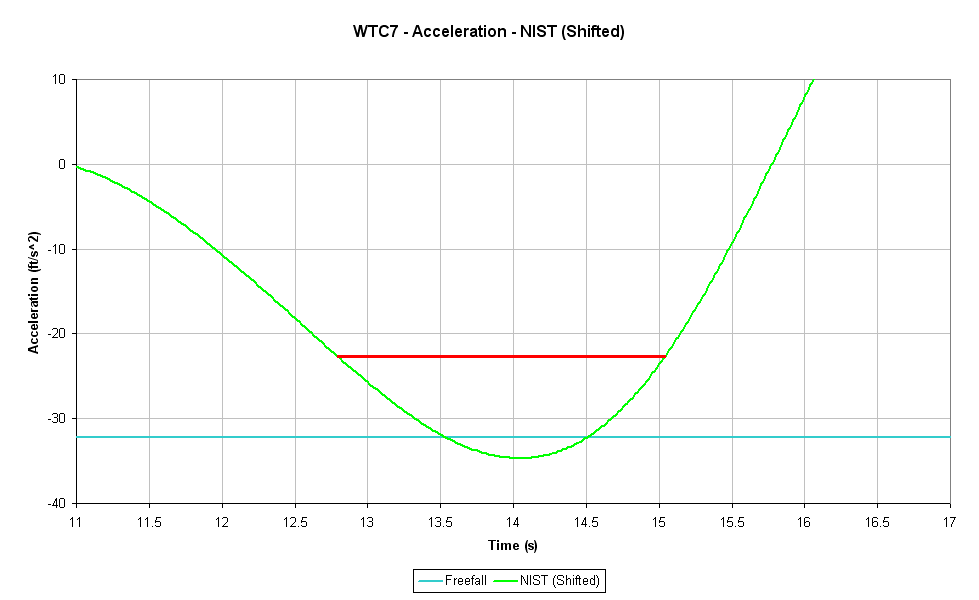
- The reasoning behind my choice of T0 (11.71s) should be pretty obvious.
- The curve implied by the NIST formula will clearly never correlate well with any of my curves over the full duration, no matter where you shift it to on the time axis.
- The steep increase in acceleration shown by all of my graphs (and tfk's) shows what happened.
- My graphs are not T0 dependant (as I have told you a few times).
Repeatedly suggesting ALL of my curves (and
tfk's) are
inaccurate between 11 and 13 seconds is based upon your particular method of determining accuracy, and
must be where you are going wrong.
If your particular method (and procedure) spits out a number saying that the green curve is a better fit to the underlying data, then, sorry, but the method is flawed. That the green curve can be made to match for a short period is irrelevant to validating the NIST formula for the purpose of determining acceleration profile. (Or more likely, the numbers it spits out are
meaningless in practice with noisy data)
Seriously: It's okay to disagree with NIST's choice of t=0. If you choose to regard a different moment as the beginning of the collapse, however, then you will have to adjust NIST's time-scaling parameter λ accordingly (and you will probably have to make slight adjustments to the other two parameters, A and k). In short, you will have to perform the same kind of least-squares minimization that NIST and I did.
See above. It
does not matter where you shift the implied NIST acceleration curve. It will
never be an even
reasonable match to the truer acceleration profile (which emerges the same regardless of the many methods myself and
tfk have used). You included a graph earlier with paramaters tuned to my data, and it would
still never match to the actual trend.
One factor we must not forget...my data relates to the NW corner, NISTs to, well,
somewhere else (see list of other NIST trace data issues).
Cavalier time-shifting of NIST's model without recalculating its parameters would be dishonest.
Do you mean like this...
the choice of 10.9 seconds as a reasonable offset between your time axis and NIST's
...and...
I came up with the 10.9 second offset by eyeball.
I have also
chosen a T
0 (11.71s) based upon the last point of inflexion of the S-B derived acceleration profile.
It is not a cavalier choice, but driven by observation of the data.
As you can see, that choice also fits consistently with the velocity and displacement data...
Obviously it is necessary to place the NIST curve
somewhere, though I do not see my own selection as being in the slightest bit cavalier. I could tend to think that of your own though.
Regardless, irrespective of where the implied NIST acceleration function curve is placed it will never be a good match, and your repeated assertions that it is more accurate during certain periods of time are simply a subjective and meaningless
sum, which if you use a little cavalier eye-balling of the graphs, you can see for yourself.