Perpetual Student
Illuminator
- Joined
- Jul 8, 2008
- Messages
- 4,852
Maths is for the details and NOT the concept.
The above is another demonstration that Sol88 has no clue about the nature of scientific evidence.
Maths is for the details and NOT the concept.
What an incredible egotistical statement to make!
And what electrostatics are real difficult are they Tusenfem

I show my 4 yr old girl the SCIENCE behind those shocks she gets when she has been playing on the trampoline and touches the metal, earths, herself to ground!!
And what electrostatics are real difficult are they Tusenfem

Maths is for the details and NOT the concept.
Sol88: You must be truly ignorant if you think that electric shocks from static electricity are examples of plasma physics.I show my 4 yr old girl the SCIENCE behind those shocks she gets when she has been playing on the trampoline and touches the metal, earths, herself to ground!!
Even this non mathematical genius found the non maths answer straight forward!
i.e. you do not need a deep understanding of plasma physics and mathematics to understand what happened!
Maths is for the details and NOT the concept.
I am making one more try to get through to you (as a non-physicist). My physics will be very general and my terminology quite loose because of my own limitations.
Let's say we have two competing theories for the crater that is so dear to your heart:
1) The electrical effect you are advocating.
2) An impact by an extra-mercurial object or objects.
OK, now to decide between the two we would not simply produce both effects in a lab and try to see which one looks more like the crater. That would prove nothing and I suspect both methods could be made to generally resemble the crater. So what now?
First, we would calculate how much charge would be needed to provide the power for the electrical effect and then look for a way such a charge could be produced. Then we would look for a mechanism for the discharge required. We would measure the discharge (power) needed to produce the crater through that mechanism. We would then determine if the scenario is feasible and its likelihood.
Second, we would calculate the size of objects and velocity needed for impacts to create the crater. Then we would determine if such objects exist or ever existed to do the job and calculate the likelihood of such collisions, again determining if the scenario is feasible and its likelihood.
Now, I am sure I left out a lot, used poor terminology and demonstrated my lack of expertise in the above description. I do not have the knowledge or ability to do any of the above activities. The point here is:
Notice my use of measure and calculate. That is mathematics!
That is how physics has been done since the days of Newton. That is how alternative hypotheses are judged. There is no conspiracy to leave out EM explanations. The math has been done and alternative 2) above is the winner. Some of the people with whom you have been debating can do the mathematics and know the answer. You cannot and do not know the answer.
Got it?
Ok let get to it!
you do the math and calculate the size and speed of the impactor and I'll do the same for the electric discharge scenario.
Deal?
Sol88: Do you have a problem with your memory? The math for the electric discharge has already been done in this thread as in this posting:Ok let get to it!
you do the math and calculate the size and speed of the impactor and I'll do the same for the electric discharge scenario.
Deal?
I will play along with the troll for a second.
Sol88, if you hypothesize that the planet Mercury was once charged up---like a great big capacitor---and that a runaway *discharge* created an arc, and the arc was responsible for the spider-like formation in the Caloris basin ... well, let's do some MATH.
Let's hypothesize that we can charge Mercury up. Just plug in a big jumper cable, or shoot a highly-charged wind at it, or ... something. One way or another, we'll hypothesize that we can build up an electrostatic voltage on the whole planet. How much excess charge can we pack on while doing this?
As an isolated sphere, Mercury's capacitance is about 0.2 millifarads. That's, um, not very much. A *gigavolt* static potential would carry only 200,000 Coulombs (about one car battery). I want to emphasize that a gigavolt is a very, very high potential. There is no way to charge something up to a gigavolt by bathing it in a kilovolt-energy solar wind.
Let's see, how much *energy* do you store when you pack 200,000 C into a gigavolt potential? 2 x 10^14 joules ... about 50 kT of TNT, or something in the ballpark of the Nagasaki atomic bomb.
Therefore, we have (unfortunately) lots of experience with the craters formed by 50 kT energy releases. They're a 100 meters in diameter and a few meters deep---underground explosions might excavate only a hundred meter or so cavity. Moving rock around takes lots of energy.
So what do we find on Mercury? A hole 40,000 meters in diameter.
Sol88, your "arc welder" hypothesis requires energy to be stored somewhere. The largest charge we can expect Mercury to pick up from the Solar Wind is a few kilovolts, giving it a few hundred Joules of energy---whereupon your Giant Arc Discharge Into Space could perhaps occur, but it would barely heat up a cup of tea, much less excavate a 40,000 meter crater.
How much energy do you think you need for the crater, Sol88? How will you charge up an isolated capacitor to the (apparently required) ten teravolts? You can't. Since Mercury could never have been this highly charged, it's never had anything like enough stored electrostatic energy to excavate a crater with an arc discharge. You casually invented an Giant Cosmic Welding Torch, Sol88, but you forgot to find somewhere to plug it in.
You're welcome to do the same calculation under the (equally stupid) assumption that Mercury had (like Earth) a dielectric atmosphere with an internal mechanical charge conveyor. You will have to learn electrostatics to do so.
Sol88: Do you have a problem with your memory? The math for the electric discharge has already been done in this thread as in this posting:
(I added a link to a source for Mercury's capacitance)
The conclusion is that realistically an electrical discarge would "barely heat up a cup of tea" and that with values that were well over the maximum expected, an electrical discarge could create a crater ~100 meters in diameter.
Question, what data did you use to calculate Mercury's capacitance?
Question, what data did you use to calculate Mercury's capacitance? And which equation was it applied too, from the LINK you supplied?
Zig is right, there's only one way to calculate the capacitance of an isolated sphere in space. This calculation is re-derived by thousands of freshman physics majors every year.
I am making one more try to get through to you (as a non-physicist). My physics will be very general and my terminology quite loose because of my own limitations.
Let's say we have two competing theories for the crater that is so dear to your heart:
1) The electrical effect you are advocating.
2) An impact by an extra-mercurial object or objects.
OK, now to decide between the two we would not simply produce both effects in a lab and try to see which one looks more like the crater. That would prove nothing and I suspect both methods could be made to generally resemble the crater. So what now?
First, we would calculate how much charge would be needed to provide the power for the electrical effect and then look for a way such a charge could be produced. Then we would look for a mechanism for the discharge required. We would measure the discharge (power) needed to produce the crater through that mechanism. We would then determine if the scenario is feasible and its likelihood.
Second, we would calculate the size of objects and velocity needed for impacts to create the crater. Then we would determine if such objects exist or ever existed to do the job and calculate the likelihood of such collisions, again determining if the scenario is feasible and its likelihood.
Now, I am sure I left out a lot, used poor terminology and demonstrated my lack of expertise in the above description. I do not have the knowledge or ability to do any of the above activities. The point here is:
Notice my use of measure and calculate. That is mathematics!
That is how physics has been done since the days of Newton. That is how alternative hypotheses are judged. There is no conspiracy to leave out EM explanations. The math has been done and alternative 2) above is the winner. Some of the people with whom you have been debating can do the mathematics and know the answer. You cannot and do not know the answer.
Got it?
Abstract
Energetic and magnetostrophic balance arguments show that a dynamo source for Mercury's observed magnetic field is problematic if one expects an Earth-like partitioning of toroidal and poloidal fields. (snip) We examine the ratio of the dipole field at the core mantle boundary to the toroidal field in the core for various shell thicknesses and Rayleigh numbers and find that some thin shell dynamos can produce magnetic fields with Mercury-like dipolar field intensities. In these dynamos, the toroidal field is produced more efficiently through differential rotation than the poloidal field is produced through upwellings interacting with the toroidal field. (sniped)
Abstract
An updated analysis and interpretation are presented of the magnetic field observations obtained during the Mariner 10 encounter with the planet Mercury on March 29, 1974. The combination of data relating to position of the detached bow shock wave and magnetopause and the geometry and magnitude of the magnetic field within the magnetosphere-like region surrounding Mercury lead to the conclusion that an internal planetary field exists with dipole moment approximately 5.1 times 10 to the 22nd G per cu cm. The dipole axis has a polarity sense similar to that of earth and is tilted 7 deg from the normal to Mercury's orbital plane. The magnetic field observations reveal a significant distortion of the modest Hermean field by the solar wind flow and the formation of a magnetic tail and neutral sheet which begins close to the planet on the night side. Presently, an active dynamo mechanism in the planetary interior appears to be favored in the interpretation of the field origin.
The observed field amplitude, however, is too weak to be compatible with typical convective planetary dynamos. The Lorentz force based on an extrapolation of Mariner 10 data to the dynamo region is 10‑4 times smaller than the Coriolis force. This is at odds with the idea that planetary dynamos are thought to work in the so-called magnetostrophic regime, where Coriolis force and Lorentz force should be of comparable magnitude. Recent convective dynamo simulations reviewed here seem to resolve this caveat. We show that the available convective power indeed suffices to drive a magnetostrophic dynamo even when the heat flow though Mercury’s core mantle boundary is subadiabatic, as suggested by thermal evolution models.
Abstract
Observations by MESSENGER show that Mercury's magnetosphere is immersed in a comet-like cloud of planetary ions. The most abundant, Na+, is broadly distributed but exhibits flux maxima in the magnetosheath, where the local plasma flow speed is high, and near the spacecraft’s closest approach, where atmospheric density should peak. The magnetic field showed reconnection signatures in the form of flux transfer events, azimuthal rotations consistent with Kelvin-Helmholtz waves along the magnetopause, and extensive ultralow-frequency wave activity. Two outbound current sheet boundaries were observed, across which the magnetic field decreased in a manner suggestive of a double magnetopause. The separation of these current layers, comparable to the gyro-radius of a Na+ pickup ion entering the magnetosphere after being accelerated in the magnetosheath, may indicate a planetary ion boundary layer.
Abstract
Mapping Mercury's internal magnetic field with a magnetometer in closed orbit around the planet will provide valuable information about its internal structure. By measuring magnetic field multipoles of order higher than the dipole we could, in principle, determine some properties, such as size and location, of the internal source. Here we try to quantify these expectations. Using conceptual models, we simulate the actual measurement during the BepiColombo mission, and then we analyze the simulated data in order to estimate the measurement errors due to the limited spatial sampling. We also investigate our ability to locate the field generating current system within the planet. Finally, we address the main limitation of our model, due to the presence of time-varying external magnetospheric currents.
Abstract
At Mercury’s surface external magnetic field contributions caused by magnetospheric current systems play a much more
important role than at Earth.They are subjected to temporal variations and therefore will induce currents in the large conductive
iron core.These currents give rise to an additional magnetic field superposing the planetary field.We present a model to estimate the
size of the induced fields using a magnetospheric magnetic field model with time-varying magnetopause position.For the Hermean
interior we assume a two-layer conductivity distribution.We found out that about half of the surface magnetic field is due to
magnetospheric or induced currents.The induced fields achieve 7–12% of the mean surface magnetic intensity of the internal
planetary field, depending on the core size.The magnetic field was also modeled for a satellite moving along a polar orbit in the
Hermean magnetosphere, showing the importance of a careful separation of the magnetic field measurements.


If a capacitor is driven with a time-varying voltage that changes rapidly enough, then the polarization of the dielectric cannot follow the signal. As an example of the origin of this mechanism, the internal microscopic dipoles contributing to the dielectric constant cannot move instantly, and so as frequency of an applied alternating voltage increases, the dipole response is limited and the dielectric constant diminishes. A changing dielectric constant with frequency is referred to as dielectric dispersion, and is governed by dielectric relaxation processes, such as Debye relaxation. Under transient conditions, the displacement field can be expressed as (see electric susceptibility):
Ben M
Enlighten me please! along with all the lurkers here, so we can see the values used.
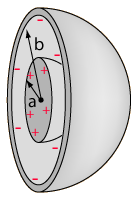
So far I've demonstrated that the core of Mercury can be inductively charged via the solar "wind" and can act as a capacitor.
The equation is [latex]C = 4\pi\epsilon_0 R[/latex]
Pi is 3.14159, a fact I don't think is in dispute.
Epsilon_0 is 8.854 x 10^-12 F/m, a constant of nature used in all electrostatics calculations.
4 is an integer, used fairly commonly in mainstream science
R is the mean radius of the sphere whose capacitance you want to calculate, or 2,439,000 meters.
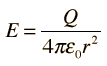
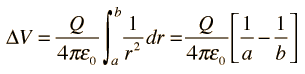
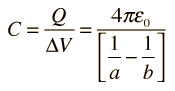
Note to students:
The philosopher H. G. Frankfurt defined "Bull****ing" as the case, distinct from truth-telling and from lying, where the speaker doesn't care what the truth-value of their statements is.
To all appearances, Sol doesn't care that he's quoted paragraph on (effectively) how Mercury's rock is a good conductor and used it to argue that it's an insulator. He doesn't care that he's quoted a divergenceless electric field and announced that it induces a charge, which is the opposite. He doesn't care whether the capacitance of the core-surface system is bigger, or smaller, or of the same order as the free-sphere capacitance ... he doesn't know what any of this means and he doesn't seem to care.
That's what Frankfurt was talking about.
glass is a good insulator!What greets astronauts and spaceships is a complex material comprising "sharp, abrasive, interlocking fragile glass shards and fragments," Taylor says. It grinds machinery and seals, and damages human lungs.

