Are there actually creationists who are scientists?

[Ichneumonwasp]

Not random.

Meaning 'no distribution'? Seems a pretty useless distinction to make when referring to biological systems, don't you think?

It would seem to me that, if that is a true 'technical definition' of 'non-random', then it can only mean 'determined' -- only a single output is possible.

Do you have a definition of "real"?

Come on, of course not. I was making a linguistic/semantic point. Though that was cute.

 

[Ichneumonwasp]

Let me make sure I have this straight.

If I alter a die to produce a six with each and every role, that is non-random. But if I'm not as good as that and a few other results show up even though I've loaded a die to try and produce a six, then those results are described by the same word as if I had never loaded the die to begin with?

If the word 'random' were telling us anything useful about a process, doesn't that strike you as strange?

 

[fishkr]

Come on-- religionists claim god came from nothing, don't they?

I think most creationists take the point of view that God has always existed. I like the Budhist "from the very no-beginning". Poetic.

M

 

[Meadmaker]

Meaning 'no distribution'? Seems a pretty useless distinction to make when referring to biological systems, don't you think?

It would seem to me that, if that is a true 'technical definition' of 'non-random', then it can only mean 'determined' -- only a single output is possible.

Correct.


[/QUOTE]
Come on, of course not. I was making a linguistic/semantic point. Though that was cute.[/QUOTE]
Thank you.

 

[Meadmaker]

Let me make sure I have this straight.

If I alter a die to produce a six with each and every role, that is non-random. But if I'm not as good as that and a few other results show up even though I've loaded a die to try and produce a six, then those results are described by the same word as if I had never loaded the die to begin with?

If the word 'random' were telling us anything useful about a process, doesn't that strike you as strange?

Perhaps describing a process with one word is a bit too simplistic?


For a mathematician, the loaded die is random, just like the non-loaded die. You can't even say that one is "more random" than the other, because the phrase "more random" is undefined. There's no such thing as "more random" in a probability textbook.

 

[Ichneumonwasp]

Perhaps describing a process with one word is a bit too simplistic?

Yeah, I think that would be the best way to look at it, especially when speaking of something as complex as biological processes.

 

[jimbob]

Would they describe highly skewed distributions as random?

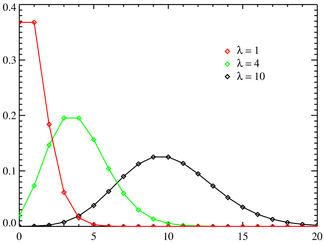
Natural selection would prbably mean that the number of reproducing offspring per parent would follow the Poisson distribution.

This can be very highly skewed.

ETA: picture added

You can make simple assumptions and calculations, even at this level of abstraction (hey I am an engineer, this is what I do)*.

In a stable population, the average number of reproducing offspring per parent would be one (i.e. lambda would be one).

An advantageous trait might have a lambda of 1.1, i.e. a 10% advantage compared to the population without that trait.

If there are 1 million offspring/parent (e.g. from a fish spawing) then this 10% advantage translates into a raised chance of reproduction for an individual fry of 10% to 1.1 per million. Still not good odds, but if you have 1 million fish, all with this trait...

*Am I right that Meadmaker, mijo, and Schneibester also have an engineering/physical sciences background too, and is this significant?

ETA:

I am thinking that as rough estimations, I try to state my assumptions, and work out fthe implications form these to get a ball-park figure. These rough calculations would involve calculations. If I would try to do this with natural selection, and don't assume something akin to the Poisson distribution, the numbers are obviously nonsensical, populations would rocket, and there would only be three states: disadvantage, neutral and advantage. The concept of a slight advantage requires a probabilistic treatment of natural selection.

In artificial selection there is no such thing as a slight advantage, one either trys to breed as many offspring from an organism as possible or none. (There is still natural selection limiting this too, of course).

 

[jimbob]

Following from my previous post (the asterisked point).

Haing read what mijo has said, I never interpereted his posts as invoking a need for supernatural intervention in evolution.

I had taken his posts as implicitly accepting a non-supernatural understinding of the origin of humanity; but because of the previous discussion I asked him, for clarification, and mijo made it explicit.

The problem with "random" is why I like "probabilistic" to describe selection, it is not wrong, but someone might have to ask for elaboration on the meaning, which would hopefully resolve any misconceptions.

 

[Ichneumonwasp]

Following from my previous post (the asterisked point).

Haing read what mijo has said, I never interpereted his posts as invoking a need for supernatural intervention in evolution.

I had taken his posts as implicitly accepting a non-supernatural understinding of the origin of humanity; but because of the previous discussion I asked him, for clarification, and mijo made it explicit.

The problem with "random" is why I like "probabilistic" to describe selection, it is not wrong, but someone might have to ask for elaboration on the meaning, which would hopefully resolve any misconceptions.

Yes, the Poisson distribution fits variation with natural selection nicely. And I never thought Mijo was a creationist either, but I didn't really care either way. People can believe whatever they want. It's the arguments that matter.

The technical definition of random just seems far too restrictive to fit with any biological system. Virtually nothing in biology is non-random using that definition, so it seems like a completely useless word to apply in biology. Especially when discussing evolution, in which nothing could possibly work without variability, I think 'random' is a very misleading term. I like probabilistic. That's a very good term for biology.

 

[jimbob]

Yes, my other point was that if I had been called a creationist and liar as many times as mijo, I'd be getting pretty narked off...

 

[articulett]

OK, but here is where you are wrong. You equate quantum indeterminacy as a basic structure of the universe and an integral descriptor of atomic movement to evolution. Evolution is not basically a 'random' process if by random you refer to quantum indeterminancy. Evolution takes place at a much higher level of description. While quantum processes may play some role, they are not the primary driving force behind variability.

'Random' as it relates to evolution and natural selection still refers to our ignorance, not to the any basic structure or explanation of its mechanisms. 'Random' in descriptions of evoluationary processes refers to the way we describe and predict outcomes -- descriptions that necessarily, for us, are probabilisitc because we lack so much knowledge of the inputs. The mistake you continually make in your descriptions is assigning 'randomness' as an integral part of the process, as though that tells us anything about the process as a whole. It doesn't. "Random' is a comment about us, not about evolution.

Per mijo's definition of random, if anything has any randomness in it, you can call it "random" or a "random process"-- since all things are made of atoms-- all things are essentially random. Really. He doesn't care about being clear--he cares the he can sum up evolution pretty close to the way Behe does--emphasize the random and make the natural selection murky and impossible to comprehend. He has shown no ability to convey how it is that the appearance of order comes from the randomness (exponential success of successful replicators... failures die out before they get a toe hold.)

 

[articulett]

Is there a technical definition of non-random? Because non-uniform, skewed distribution is the very definition of non-random out in the real world.

Mijo says that anything having to do with probability is random... anything! And if something has an randomness it it, you can characterize it as random. But no peer reviewed papers define random as they do-- the ones I found had a much stricter definition-- and they were peer reviewed. And, of course, no peer reviewed paper says Evolution IS random nor does it say natural selection is random-- creationists and apologists do this silly obfuscation dance where they make "random" encompass just about everything... and then they insist on using it to describe evolution without ever conceding that it's misleading and doesn't explain anything. It skips right over natural selection, and neither Meadmaker nor Mijo can really explain it-- it's just words that say nothing. It's just like Behe. And then they get mad when you call them on it....(also like Behe). Jim Bob thinks he's explaining it better, but while he's clear-- the majority of scientists tend to say evolution is "random (relatively) mutation coupled with natural selection which is determined (opposite of random) by the best replicators in the prior generation. I think that, like Behe, they are pretending to be academically rigorous and technical without saying anything at all. I mean Behe does that whole emphasis of random and misses the entire meat of Darwins theory. Because he knows that understanding it means that it doesn't sound implausible after all... and no designer, is therefore necessary.

Good luck. I think their conversation reads pretty much like Behe's. I've begged them to tell me the difference or to explain how the order comes from the randomness--to no avail. So you try... and see what you think. I think they are just trying to prove that they are right and thus creationists are right when they say "scientists think this all happened by chance". I don't know why anyone who wanted a useful explanatory model would describe it so unclearly. My guess is because they don't understand it-- or they don't want others too. But this is what creationists do that is so maddening. They just never say anything but they infer nasty things about scientists and others who actually could teach them something while everlastingly congratulating themselves on some weird moral authority while missing the point entirely. (Read Behe's blog and amazon.)

And why would it matter if I called them an apologist or creationist? Why wouldn't they make an effort to clarify their explanation of natural selection or agree that it's pretty vague and misleading to call it random.

It's not you. It's them. And like Kleinman and Hewitt they'll drag it on as long as you go--defending Behe and dishonesty with nary a flinch while casting aspersions upon actual scientists and actual clear explanations such as yours. The more you talk to them, the less you will feel you understand their point.
-- and when you get exasperated meadmaker will pretend he's being moral and forthright and the blather will continue.

Suffice to say, it's why creationists make very poor scientists. Their aim is to obfuscate understanding-- (so they can insert their designer in the gaps)-- not to clarify. Science clarifies information so that we can gather more information.

 

[articulett]

Perhaps describing a process with one word is a bit too simplistic?


For a mathematician, the loaded die is random, just like the non-loaded die. You can't even say that one is "more random" than the other, because the phrase "more random" is undefined. There's no such thing as "more random" in a probability textbook.

Not true. In fact, even random number generators only generate pseudo random numbers... and you nothings is truly random in a world where events are preceded by causes-- You have provided no text that would call a loaded die random. You can toss it "randomly"-- but the result is unlikely to be random--the more tosses, the less random. But this alone should make you admit that it's a bad word, but you Behe and Mijo are obsessed with using it to describe evolution in it's entirety. The majority of biologists disagree-- peer reviewed papers disagree. But you just keep assuming you are saying something no matter how vague and misleading others tell you your descriptions are. They are as useful as Behe's definitions-- useful for confusing the issue. Now why would you be interested in doing that? And doesn't that make the answer to the question in the OP --not any good scientists.

I don't know about you--but as for Mijo, you've let your hubris get in the way and now you can't see what you've become. A mealy mouthed, self important, holier than thou, Behe clone who clarifies nothing on the subject of evolution, but is convinced you know more than Dawkins, et. al. It makes me giggle.

 

[articulett]

Following from my previous post (the asterisked point).

Haing read what mijo has said, I never interpereted his posts as invoking a need for supernatural intervention in evolution.

I had taken his posts as implicitly accepting a non-supernatural understinding of the origin of humanity; but because of the previous discussion I asked him, for clarification, and mijo made it explicit.

The problem with "random" is why I like "probabilistic" to describe selection, it is not wrong, but someone might have to ask for elaboration on the meaning, which would hopefully resolve any misconceptions.

But that's your hubris. You haven't dealt with them. You haven't heard and read Behe or demski or any of those clowns. They really do sound the same. And they convince a couple of people because they sort sound like they are saying something. But so does Kleinman. So does Hewitt. If you can't nail down what they are saying and the experts seem to be describing it differently or telling them they are being vague-- what conclusion do you make. Why the need to sum up evolution in terms of "randomness" when the meat of Darwins theory had little to do with the randomness and everything to do with selection-- which organisms got to pass their info. on into vectors that would take it in to the future?

I mean you're nice and trying to make friends, but your explanation is just not clear or clean or simple-- Cyborgs was. Dawkins was. Ichneumonwasp was-- and many dropped by that other thread to say pretty much what they said-- what I said-- but it goes in one ear and out the other. Sure you can describe it however you want-- but you might want to get someone who understands the process to evaluate whether they think you are being clear. I pass board exams on this subject. You would fail.

 

[mijopaalmc]

Per mijo's definition of random, if anything has any randomness in it, you can call it "random" or a "random process"-- since all things are made of atoms-- all things are essentially random. Really. He doesn't care about being clear--he cares the he can sum up evolution pretty close to the way Behe does--emphasize the random and make the natural selection murky and impossible to comprehend. He has shown no ability to convey how it is that the appearance of order comes from the randomness (exponential success of successful replicators... failures die out before they get a toe hold.

Will someone please inform articulett that stochastic processes know as Galton-Watson processes display exactly the same behavior that she described in her last sentence and were developed to study the extinction of aristocratic surnames (or the evolution of the population of aristocratic surnames) in Victorian England?

Here is a link that shows how Galton-Watson processes have been used to study the evolution of DNA sequences:
Applications of the Galton-Watson process to human DNA evolution and demography

 

[articulett]

Randomness versus unpredictability

Randomness is an objective property. Nevertheless, what appears random to one observer may not appear random to another observer. Consider two observers of a sequence of bits, only one of whom has the cryptographic key needed to turn the sequence of bits into a readable message. The message is not random, but is for one of the observers unpredictable. One of the intriguing aspects of random processes is that it is hard to know whether the process is truly random. The observer can always suspect that there is some "key" that unlocks the message. This is one of the foundations of superstition and is also what is a driving motive, curiosity, for discovery in science and mathematics.

Under the cosmological hypothesis of determinism there is no randomness in the universe, only unpredictability.

Some mathematically defined sequences exhibit some of the same characteristics as random sequences, but because they are generated by a describable mechanism they are called pseudorandom.

Chaotic systems are unpredictable in practice due to their extreme dependence on initial conditions. Whether or not they are unpredictable in terms of computability theory is a subject of current research. At least in some disciplines of computability theory the notion of randomness turns out to be identified with computational unpredictability.

Randomness of a phenomenon is not itself 'random'. It can often be precisely characterized, usually in terms of probability or expected value. For instance quantum mechanics allows a very precise calculation of the half-lives of atoms even though the process of atomic decay is a random one. More simply, though we cannot predict the outcome of a single toss of a fair coin, we can characterize its general behavior by saying that if a large number of tosses are made, roughly half of them will show up "Heads". Ohm's law and the kinetic theory of gases are precise characterizations of macroscopic phenomena which are random on the microscopic level.

 

[jimbob]

Jim Bob thinks he's explaining it better, but while he's clear-- the majority of scientists tend to say evolution is "random (relatively) mutation coupled with natural selection which is determined (opposite of random) by the best replicators in the prior generation. I think that, like Behe, they are pretending to be academically rigorous and technical without saying anything at all. I mean Behe does that whole emphasis of random and misses the entire meat of Darwins theory. Because he knows that understanding it means that it doesn't sound implausible after all... and no designer, is therefore necessary.

How am I not being technical? I am stating the probable distribution, likely levels of advantages for a trait, which allows an assessment of the outcomes, and how likely they are.

Why make it harder for us more numerate people to understand by introducing something that is obviously wrong, when a slight change in language is not incorrect yet shouldn't confuse the non-technical etiher?

Remember the poor engineer.

By obviously wrong, I mean the following:

These rough calculations would involve calculations. If I would try to do this with natural selection, and don't assume something akin to the Poisson distribution, the numbers are obviously nonsensical, populations would rocket* , and there would only be three states: disadvantage, neutral and advantage. The concept of a slight advantage requires a probabilistic treatment of natural selection.

In artificial selection there is no such thing as a slight advantage, one either trys to breed as many offspring from an organism as possible or none. (There is still natural selection limiting this too, of course).

*Or plumet, or stay the same; oscillations and random variations would not be "allowed" (if the description was taken completely literally. If this description is "rhetorically" true, it would be better to find something that can be taken literally, may I suggest "probabilistic" )

Red text means I have edited my own quote...

 

[jimbob]

A selective advantage in a peppered moth in being camoflagued doesn't affect the ability of its offspring to find food, only to not be eaten.

A better colour scheme doesn't affect its predation by animals that use echolocation.

There might be reduced bird predation, but the reproductive success conferred by the colour scheme is probabilistic.

Such a trait is likely to spread, but not as efficiently (i.e. as fast) as if there was artificial selection for colour.

 

[articulett]

Yes, my other point was that if I had been called a creationist and liar as many times as mijo, I'd be getting pretty narked off...

Rest assured-- I've been called worse-- and called it first. I don't think I called Mijo a liar. But he is dishonest. I have never called anyone here a liar first. And I will put my word next to their word any day, any time.

Who cares if I think someone is a creationist or apologist. Are these bad words? Wouldn't they just disappear if the person actually spoke to intelligent people and they could make sense of him. No offense, but you and Meadmaker are Mijo's biggest cheerleaders, and you can't sum him up nor are you very good at describing natural selection. You think you are being clear, but you have no evidence that you are. There is no evidence to think that you could explain evolution to anyone. Whereas, Mijo et. al. have repeatedly insulted others who can and do explain evolution-- Dawkins even. Do you know how Mijo sounds different than Behe? The differences in his claim or insistence on summing up evolution as random.

And most icky, is this weird hubris that you think you'd "know" a creationist argument or how they argue or why this can't be used to obfuscate--and yet everyone who has ever engaged creationists will tell you otherwise. And who cares what anyone is? Are they saying anything useful or true?-- Are they furthering understanding? What is their goal and what is the readers?

I know you think poor mijo has been picked on by me-- but people get sick of the spin, apologies, blither, lies-- and just because you don't see it-- doesn't mean it isn't there. I'm sure you would be sticking up for Behe too. People who don't wade in this muck, are readily influenced into thinking that such people are on the up and up-- even though they can never summarize what the person they are defending is saying--what the point is. You guys are just all over the place. You did that on the other thread where Mijo asked his insincere question about the non-random aspects of evolution and refused all answers except a couple of apologists who don't make much more sense than he does-- not as far as I can tell. Why are you guys so vague and mealy mouthed when it comes to HOW the appearance of design or direction (or "order") comes about? Why? If you can't convey that, you've got a useless definition-- unless the Discovery Institute is hiring. Instead of getting hissy-- get a clue. Learn from those who HAVE described evolution. Read Darwin. Modify your explanation. Read Behe. Make sure you don't sound like him-- or expect those who have seen it all too much to call you on it.

Poor misunderstood Mijo-- he's started inane threads asking creationist questions and every one of his questions is bizarre and mealy and infers an answer-- then people go out of their way to explain things and he rejects all their explanations yet again to tell us all how technically right and academically rigorous he is. Poor Mijo. Then he obfuscates further and whines about people like Dawkins who could give him a clue and refused to look at any links that actually answer his question-- he doesn't acknowledge them and has no curiosity about the answers to his question. Poor Mijo. He has never once contributed information or dialogue of value to this forum or any decent back and forth yet he's stalked threads to vilify people who dared to call fundamentalist brainwashing "child abuse". Poor Mijo. He has no sense of humor while congratulating himself on his cleverness and bending anyone's ear who will listen to tell them how "there is no evidence that evolution is non random" (yes he said that) and other things that are thick words that say nothing.

Instead of sticking up for Mijo, why don't the both of you get a clue--actually read Darwin, Dawkins, Talk Origins, and the many brilliant and insightful people on this forum who have spent hours answering your questions. You guys are just so blind to what you can learn while insisting that you have something to teach.

What is it? What are you saying.? Who find your descriptions of evolution useful and for what? Who teaches or publishes in peer review using words the way you guys do. No one. And your egos are keeping you from actually getting a clue. Listen to ichmeunowasp, et. al.--they are much clearer and smarter and up on the subject than you--really-- way clearer than meadmaker-- and, especially, mijo. You have nothing to teach on this subject and you are sticking up for someone with enough hubris to stand up for himself. Why?

 

[articulett]

A selective advantage in a peppered moth in being camoflagued doesn't affect the ability of its offspring to find food, only to not be eaten.

A better colour scheme doesn't affect its predation by animals that use echolocation.

There might be reduced bird predation, but the reproductive success conferred by the colour scheme is probabilistic.

Such a trait is likely to spread, but not as efficiently (i.e. as fast) as if there was artificial selection for colour.

Nobody would call this random. http://www.msnbc.msn.com/id/19733274/
It looks designed... like the butterflies must have known to change-- but that's not what happened. Did the result come about randomly?-- no. Did it come about with probability-- uh, kind of-- but what a lame ass way to say it. The males carry the mutation because they were descended from one male who got a random mutation that just happened to fight of the parasite--and those who got it from him brought the population back with their descendants. THAT is natural selection. It's just mealy mouthed and useless to call THAT probabilistic or random. It doesn't explain what we observe. It doesn't convey natural selection. I've said it before and I'll say it again--that is why nobody will get anything from your explanations no matter how much you tell us it's super duper or technically correct. If you can't describe how we get this seeming "miracle" then you have a loser of a definition. If you need to squeeze the word random or something about probabilities into your story, you are obfuscating unnecessarily. Why?

So what is your goal? Is it to have a useful way of convey information--or just assert that you are right and articulett is a big meanie and Evolution is SO random-- because random means "all things having to do with probabilities." Maybe on Planet Vague-- but not for those who seek clarity.