Loss Leader
I would save the receptionist., Moderator
For Days 2–99, the probabilities are well-approximated by a cubic function (click for larger view):
I don't know what it means, but it's exactly the kind of graph I was hoping for.
For Days 2–99, the probabilities are well-approximated by a cubic function (click for larger view):
I don't know what it means, but it's exactly the kind of graph I was hoping for.
Your formula gives a probability on day 3 of 0.0433416528 which differs significantly from my 0.11526
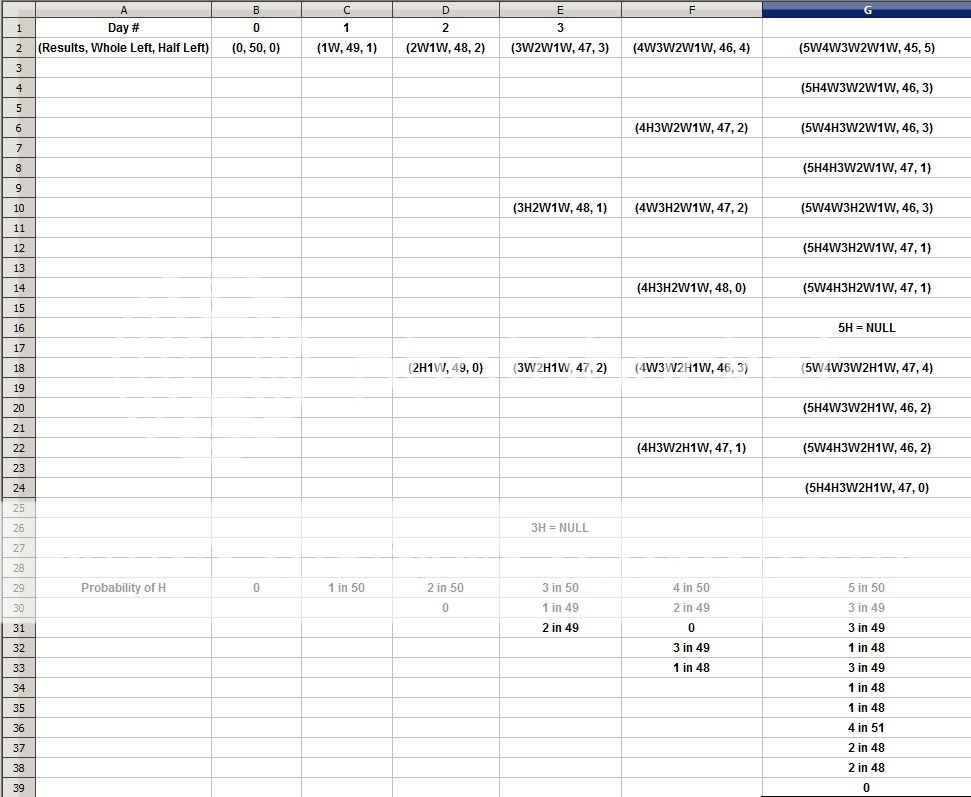
So...
2 3 4
0.02649194 0.04336187 0.05987492;;; Exact solution after n days is given by (P n) where P is
;;; defined by
(define (P n)
(Q 50 0 n))
;;; Starting from an initial state with the given number of full
;;; and half pills in the bottle, returns the probability of
;;; getting a half pill after n more pill-taking operations.
(define (Q full half n)
(if (= 0 (+ full half))
(error "You've run out of pills."))
(if (= n 0)
(/ half (+ full half))
(let* ((probability-of-half (/ half (+ full half)))
(probability-of-full (- 1 probability-of-half)))
(+ (if (= probability-of-half 0)
0
(* probability-of-half
(Q full (- half 1) (- n 1))))
(if (= probability-of-full 0)
0
(* probability-of-full
(Q (- full 1) (+ half 1) (- n 1))))))));;; This program is written in R7 Scheme ( www.scheme-reports.org )
;;; with the (r6rs hashtables) library ( snow-fort.org ).
(import (scheme base)
(scheme write)
(r6rs hashtables))
;;; Problem posed by Loss Leader at International Skeptics Forum,
;;; 10 June 2015 (Stats Question for Stats People - Pill Bottle):
;;;
;;; I have a pill bottle with 50 pills. I take half a pill a
;;; day. Each day, I shake the bottle. If I get a half-pill, I
;;; take it. If I get a whole pill, I cut it in half, take one
;;; half and put the other half back in the bottle.
;;;
;;; Assume no physical limitations such as density or sorting or
;;; layering or whatever. As between a whole and a half, they
;;; have the same likelihood of being randomly selected.
;;;
;;; Now, I know that on day 1, the chance that I will get half a
;;; pill is 0%. On day 100, the chance that I will get half a
;;; pill is 100%.
;;;
;;; What I would like to know is the chance each day of getting
;;; half a pill.
;;; Exact solution after n days is given by (P n) where P is
;;; defined by
(define (P n)
(Q 50 0 n))
;;; Starting from an initial state with the given number of full
;;; and half pills in the bottle, returns the probability of
;;; getting a half pill after n more pill-taking operations.
(define (Q full half n)
(if (= 0 (+ full half))
(error "You've run out of pills."))
(if (= n 0)
(/ half (+ full half))
(let* ((probability-of-half (/ half (+ full half)))
(probability-of-full (- 1 probability-of-half)))
(+ (if (= probability-of-half 0)
0
(* probability-of-half
(Q full (- half 1) (- n 1))))
(if (= probability-of-full 0)
0
(* probability-of-full
(Q (- full 1) (+ half 1) (- n 1))))))))
;;; Given a procedure of three arguments, returns a similar procedure
;;; that records its arguments and results in a table so it never has
;;; to do the same calculation again.
(define (memoized f)
(let ((ht (make-hashtable equal-hash equal?)))
(lambda (x y z)
(let* ((args (list x y z))
(probe (hashtable-ref ht args #f)))
(or probe
(let ((result (f x y z)))
(hashtable-set! ht args result)
result))))))
(set! Q (memoized Q))
;;; The following loop performs all calculations using exact rational
;;; arithmetic but displays the results in decimal scientific notation.
;;; In implementations that represent inexact reals using IEEE double
;;; precision, the printed results are accurate to 53 bits.
(do ((n 0 (+ n 1)))
((= n 100))
(display (substring (number->string (+ 1000 n)) 1 4))
(display " ")
(write (inexact (P n)))
(newline))000 0.0
001 0.02
002 0.0392
003 0.05765616326530612
004 0.07541917374427322
005 0.09253492703745321
006 0.10904511473367409
007 0.1249877216072071
008 0.14039745104999926
009 0.1553060909817548
010 0.1697428300725786
011 0.18373453224124375
012 0.19730597592349589
013 0.2104800634423788
014 0.22327800488520572
015 0.2357194801465704
016 0.24782278219388637
017 0.2596049441211212
018 0.27108185215449204
019 0.28226834644299986
020 0.29317831119286825
021 0.30382475547727883
022 0.3142198858626351
023 0.3243751718330737
024 0.33430140486060445
025 0.34400875185469165
026 0.35350680362872866
027 0.3628046189388262
028 0.37191076458027045
029 0.3808333519669855
030 0.38958007056776894
031 0.3981582185286499
032 0.4065747307723589
033 0.41483620483269806
034 0.42294892465280626
035 0.4309188825512912
036 0.43875179953843
037 0.44645314414566845
038 0.45402814991510926
039 0.4614818316812539
040 0.4688190007646809
041 0.47604427918639375
042 0.4831621130020481
043 0.4901767848470315
044 0.4970924257762721
045 0.5039130264766016
046 0.5106424479243951
047 0.5172844315569937
048 0.52384260902304
049 0.5303205115742737
050 0.5367215791595469
051 0.5430491692808213
052 0.5493065656707092
053 0.5554969868517861
054 0.561623594639459
055 0.5676895026527533
056 0.5736977849010553
057 0.5796514845198124
058 0.5855536227346281
059 0.5914072081413518
060 0.5972152463999946
061 0.6029807504529994
062 0.6087067513941056
063 0.6143963101334219
064 0.6200525300282556
065 0.6256785706788104
066 0.631277663124526
067 0.6368531267224323
068 0.6424083880458785
069 0.6479470022135948
070 0.6534726771495076
071 0.6589893013888216
072 0.6645009761933173
073 0.6700120529292033
074 0.6755271769087903
075 0.6810513392230929
076 0.6865899385249656
077 0.6921488553026562
078 0.6977345419712979
079 0.7033541331926046
080 0.7090155823419024
081 0.7147278321767083
082 0.7205010308304748
083 0.7263468087556949
084 0.7322786389460653
085 0.7383123130893086
086 0.7444665821694477
087 0.7507640368491393
088 0.7572323422998845
089 0.7639060329896881
090 0.770829133016293
091 0.7780594631636658
092 0.7856743620418761
093 0.7937868043733781
094 0.8025413029600896
095 0.8122928158296366
096 0.8229116122613481
097 0.8388398069089154
098 0.8388398069089154
099 1.0