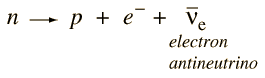Null Physics anyone?

[Reality Check]

I agree that on this point Witt has been misinterpreted. The extract only talks about bound electrons in the nucleus (not free neutrons). It does not state that neutrons are protons and electrons. It is strange though that the last diagram for a neutron star is described as "two protons and two bound electrons, a neutron doublet".

Leonard Susskind, lee Smolin, David Greene etc etc did not need to put their books through peer review. Peer review is not for books, it is for scientific papers. But the contents of their books are based on scientific papers with a bit of speculation mixed in as is proper for popular books.




There are other issues with null physics. When I get his book I will be in a position to comment better. The issues I can see now are:

• There is no zero-point energy in null physics.
  But there are experimentally verified effects (Casmir Effect, Lamb Shift) that rely on there being a zero-point energy.
  
  
• No black holes in null physics. It does not allow matter to compress further than the "core repulsion" of neutrons.
  
  There is a lot of evidence for things that look like supermassive black holes in the center of many galaxies including ours. Null physics does have hypermassive objects. From my last posting in his forum:
  

  The point of the quote from Wikipedia was not really about the supermassive black hole in our galaxy. It was that any mass with the density of water over 150,000,000 solar masses will have a Schwarzschild radius that is greater than its radius. Supermassive objects up to 18 billion solar masses have been observed. Many of these objects have masses over 150,000,000 solar masses and so are counter-examples to your calculation for Sag A* in that they do not have mass that extends outside of their Schwarzschild radius.
  
  So now we have 2 types of supermassive objects: hyperdense objects with mass outside of the Schwarzschild radius (and no event horizon?) and supermassive black holes whose mass lies inside their Schwarzschild radius and thus have event horizons.

  
  
• The null physics explanation for the cosmological redshift ("intergalactic redshift" in the book is lumetic decay. This is the gravitational redshift caused by the universal gravitational field in a flat universe.
  
  But gravitational redshift depends on the gravitation field changing (see Wikipedia).
  Thus we would need a non-uniform gravitational field of the universe that increases in all directions from the observer to give a redshift that increases with increasing distance. This allows the light to climb "uphill" out of a gravity well to the observer and thus redshift in all directions. This makes that observer privileged which is not allowed in GR.
  Alternately every observer will deduce that the density of matter in the universe increases as distance increases from them.
  
  
  
• He has a white paper called "Einstein's Nonphysical Geometry" where he derives an equation stating that the % change in radial length diverges far from a Schwarzschild radius.
  
  I think that he is using infinity improperly since using the exact solution (see equation 8) for the change in the Schwarzschild coordinate r gives the percentage change as (infintity - infinity)/infinity.
  
  He uses an approximation that starts with the statement "In the limit (R2 − R1) → dr" where R1 and R2 are 'radial lengths' and dr is an infintesimal change in the Schwarzschild coordinate r. This looks incorrect since it assumes that r is a radial length which is is not.
  Just below equation 8 in the above paper:
  

  The coordinate r is an “areal” radius — it labels spherical surfaces of area 4πr², but it does not label proper distance in a simple way.

 

[Paulhoff]

A proton can change into a neutron by electron absorption.
It's not wrong to say that the proton and electron are building blocks.
Whats your point?
For goodness sake the hydrogen atom is the basic building block, add electrons one by one and you get the list of elements

You don't read do you, that is not the only way......

Inside of a bound nucleus, protons can also transform via beta decay into neutrons. In this case, the transformation may occur by emission of a positron (antielectron) and neutrino (instead of an antineutrino):

It is wrong to say that protons and neutons are building blocks when you know about quarks.

Paul

 

[Skwinty]

Sure, I never read the article. I answered off the cuff.
Yes, you are right quarks are the preferred building blocks.
It is just a more complex and convoluted way of describing things.
What does a quark consist of?
We know that a quark is a hypothetical particle but what makes a quark.
And then when you know that particle you can ask what makes that particle ad infinitum.

So what at the end of the day is the true building block?
Another hypothetical particle?

 

[sol invictus]

I think the issue really stems from the fact that Witt chose to represent the neutron pictorially with round circles representing the proton and the electrons as little circles bound into the circle representing the neutron.
You must admit it is easier to draw that than the up/down quarks etc.
Now to use that issue to dismiss him as a crackpot is really splitting hairs.
.

Splitting hairs???



The bound state of a proton and an electron has a name... it's called a hydrogen atom. Heard of those?

If the neutron were a bound state of a proton and an electron (with or without the anitneutrino, take your pick) its decay would violate conservation of energy.

All this stuff has been quite well understood since the 1930's.

 

[sol invictus]

The neutron decays in a few minutes to a proton + electron + electron anti-neutrino.
So wheres there no proton and electron?
I have yet to see where Witt makes the claim that the neutron only consists of a proton and electron.

(my emphasis)

SH: No, I'm saying that the conversion of an electron from its free state to its neutronic bound state requires the absorption of an (anti)neutrino. This is mentioned in the book that no one on this blog has read yet.

Sh: The decay of a neutron involves the emission of a proton, electron, and (anti)neutrino. I trust you agree that spin is conserved during this beta decay process. The formation of a neutron would necessarily, by time symmetry, involve the combination of an electron, proton, and absorption of a (anti)neutrino as part of the electron binding process.
<snip>

By the way, in quoting that I noticed something rather interesting...

Sh: The decay of a neutron involves the emission of a proton, electron, and (anti)neutrino.

<snip>

LL: If you read the prior posts, it should answer most of your questions.

Ben M:
To put Bens opinion in perspective.

<snip>

Sol:Actually we have a very good answer for that - symmetries are fundamental.

How interesting - a new poster suddenly appears and starts promoting Witt's book. Oddly, our new friend uses an unusually quoting style, strangely reminiscent of the one used by Mr. Witt himself....

Anyone smell dirty socks?

 

[Skwinty]

How typical of you Sol.
Trash any opposition. You are the epitomy of an arrogant ,chauvinistic and self hailed expert.
The only reason I quoted like that was because I was offline when i composed the post.
I had save the thread pages earlier.
I had never heard of Witt until last week, have not bought his book and am not defended him.I am taking issue with people like you who feel that it is your duty to trash any one whose opinion is not in line with your own

 

[Skwinty]

also, where does he say that the neutron consists only of a proton and an electron??

 

[sol invictus]

also, where does he say that the neutron consists only of a proton and an electron??

Are you incapable of reading? As I said, add the antineutrino if you like: It doesn't make any difference.

The formation of a neutron would necessarily, by time symmetry, involve the combination of an electron, proton, and absorption of a (anti)neutrino as part of the electron binding process.

If this were correct, the decay of the neutron would violate conservation of energy. This is high school level physics - evidently Mr. Witt doesn't understand the meaning of "bound".

 

[sol invictus]

How typical of you Sol.
Trash any opposition. You are the epitomy of an arrogant ,chauvinistic and self hailed expert.

When someone comes here with garbage, it gets put right where it belongs - in the trash. That's just as it should be. If you can't take it, leave.

I had never heard of Witt until last week, have not bought his book and am not defended him.

Sure.

I am taking issue with people like you who feel that it is your duty to trash any one whose opinion is not in line with your own

It's not an opinion. Ever heard of facts? Science? Basic Aristotelian logic?

 

[Skwinty]

These are the facts about neutron decay.
Perhaps you should take your own advice!



The present understanding of the decay of the neutron is

This decay illustrates some of the conservation laws which govern particle decays. The proton in the product satisfies the conservation of baryon number, but the emergence of the electron unaccompanied would violate conservation of lepton number. The third particle must be an electron antineutrino to allow the decay to satisfy lepton number conservation. The electron has lepton number 1, and the antineutrino has lepton number -1.

 

[sol invictus]

These are the facts about neutron decay.

Yes, your cut and paste is correct - and it immediately proves that the neutron cannot be a bound state of a proton and an electron (or of a proton, electron, and antineutrino). A bound state - by definition - has less energy than the sum of its constituents. If the neutron were such a bound state, that decay would violate conservation of energy.

As I mentioned, this has been understood at least since 1934 when the mass of the neutron was measured accurately. But it's news to Mr. Witt, apparently.

 

[ben m]

Skwinty, there are lots of reasons to say a neutron is not a proton+an electron. First of all, accelerator experiments show that the following reactions all have the exact same probability (modulo a universal phase-space factor):

antineutrino + proton -> neutron + positron
neutrino + neutron -> proton + electron
neutron + positron -> antineutrino + proton
proton + electron -> neutrino + neutron

If the electron is somehow "already" inside the neutron, doesn't the above data suggest that the positron is (in the same way) "already" in the proton?

If there's already an electron inside the neutron, shouldn't it be possible to get it out by smashing something into it? Unfortunately, although reactions like :

p+ p+ --> n0 p+ pi+
n0 p+ --> n0 n0 pi+
n0 p+ --> p+ p+ pi-
n0 n0 --> n0 p+ pi-

are extremely high-probability and have identical cross sections, reactions like this:

p+ n0 --> p+ p+ e- antineutrino
p+ p+ --> p+ n0 e+ neutrino

are extremely rare ... but again have identical cross sections. (Replace that p+ projectile with an electron beam, and you're looking at some of the most-precise nuclear physics experiments ever performed.) Why should the first reaction---which Witt's theory would describe as "knocking an electron out of a neutron"---have exactly the same cross-section as the second one, which Witt could only describe as "creating a positron out of thin air"? The standard quark-model (or the predecessor isospin model) said: "except for something carrying a charge difference, protons and neutrons have exactly the same constituents"; that's a good answer. "Neutrons are different than protons because there's an electron inside them, and I'll invent something later that explains why they look identical in every possible process except neutron decay" is a really bad answer.

This is the standard crackpot mistake, Skwinty. You (and Witt) behave as though the standard model is a complex explanation for a simple phenomenon; that the "phenomenon" in need of explaining is the simple thing you learned in high school (in this case "the neutron is slightly heavier than, and decays to, p+ e-"); and that all of the additional information gathered by Mainstream Physicists is a heap of trivia ("splitting hairs" as you say) that can be dealt with later by some pedant or another.

You're declaring that your neutron model is a reasonable one without, to all appearances, having read one single article or textbook chapter on actual measurements involving neutrons. That's what makes it crackpottery---the complete disconnect from what ought to be relevant data.

 

[godless dave]

I also understand that the work on theoretical physics continues albeit with an incessant request for bigger and better colliders and equipment.

That's because hypotheses have to be tested to be accepted.

Yes, you are right quarks are the preferred building blocks.

Preferred? Reality isn't subject to our preferences.

It is just a more complex and convoluted way of describing things.

It's also more accurate.

 

[Tubbythin]

Hi Tubbythin
The splitting hairs comes about from this.(I thought my previous post was clear though)

You trash Witt because you say that a neutron doesnt contain a proton and an electron.
A neutron will decay to a proton , electron and electron antineutrino in about 10 minutes.

Yes. Which in itself is very good evidence for the neutron not being composed of a proton and an electron (and an antineutrino). The fact that it takes so long is because the Q value is pretty small and it is a weak interaction. It is a weak interaction because there is a quark flavour change from d to u. If there were no quark flavour change (eg if the neutron was a proton and an electron stuck together) then the decay would proceed much much faster.

I also stated that there is a difference between particle bombardment,fission,fusion and radioactive decay and therefore different results to the processes.
Sure when you smash particles together you can count and describe the bits and end up with quarks etc.
This is not the case in fission,fusion or decay.So, where is the fail to the power of four come into the equation.

Actually, studies using fusion-evaporation reactions often do precisely that. If you're looking for an exotic nucleus with a small production cross-section one of the best ways to remove contamination from competing channels is to observe the evaporated particles (protons, neutrons, alphas).
The point I was making was that none of bombardment, fission, fusion or radioactive decay give any evidence whatsoever for the neutron being composed of a proton and an electron.

With respect to neutron stars, what would the correct term in your opinion be? Fuse is good enough for me.

In a normal nucleus its called electron capture. Fuse implies a bound state of the initial constituents.

As far as the LHC is concerned, it has not smashed anything as yet,but the upgrades are already planned.The fact of the matter is that no LHC will ever be large or energetic enough to emulate the conditions in the cosmos.

Which conditions? The cosmos is at ~3 K so you need to be a little more specific.

I will believe the existence of the Higgs when and if it is discovered.

Fair enough.

You may find it easier to rebutt arguments by implying that I do not know what I'm talking about as it is easier than using logic and fact.

The facts I am using are that there is no evidence to suggest the neutron is a composite of proton and electron and that there is plenty of evidence to suggest it is not. The logic I am using is that given the previous sentence, it is a waste of time considering Witts book.

You say that Witts theory contradicts observation.
Given that you have read the excerpts, I think that Witt is offering a different interpretation of these observations and not disputing the observations.

You dont specify what your profession is in your public profile.
Would you like to share this information?

I'm a nuclear physics PhD student.

 

[Tubbythin]

Yes, you are right quarks are the preferred building blocks.
It is just a more complex and convoluted way of describing things.

No. Its the simplest way of describing observations.

What does a quark consist of?
We know that a quark is a hypothetical particle but what makes a quark.
And then when you know that particle you can ask what makes that particle ad infinitum.

As far as we can measure, nothing. And no, the quark has been more than just hypothetical since the late 1960's.

So what at the end of the day is the true building block?
Another hypothetical particle?

Thats one of the questions particle physicists are trying to answer. By building new accelerators that you seem to have a thing against.

 

[Skwinty]

Hi All
First of all I want to restate a few things again.

1. I have no connection whatsoever with Witt, so to be called a smelly sock puppet doesn't go down well with me. What would I stand to gain by trying to promote his book amongst all you learned folk.
2. I am not a physicist of any kind, merely an electrical engineer in the nuclear instrumentation and control arena.
3. My questions and sometimes hostile statements come from the fact that the dismissing of Witt as a crank seems to be unfair.
He clearly states that he is presenting a philosophical theory that wants to get away from the standard model and then work towards a scientific theory.
4. The issue of the neutron beta decay clearly is one pertaining to the unbounded neutron. Now if the neutron consists of quarks of different flavours and protons consist of quarks of different flavours there is huge commonality between them. ie the same components with different characteristics. Therefore the assumption that the neutron has the building blocks of the proton electron and electron antineutrino is not unreasonable.
5.At last you folk are beginning to rebutt using logic and fact instead of facetious one liners. I appreciate that.
6.Some of you may or may not buy his book for further investigation.
It is not fair to trash him based on the excerpts. But there again as he says, any theory presented for peer review that is not consistent with the current paradigm will be rejected poste haste.
7. I dont have anything against the LHC or any scientific endeavours, merely some scepticism that these are going to produce the answers to everything or even most of every thing.
8.As I said in a previous post, it seems as though the philosophy of science died with Einstein.
9. When it comes to energies that can be generated on earth, even the simultaneous explosion of all the nuclear bombs ever created would pale in comparison to the energies that exist in the cosmos.

Thanks for the discussion

 

[DeiRenDopa]

... snip ...

6.Some of you may or may not buy his book for further investigation.
It is not fair to trash him based on the excerpts. But there again as he says, any theory presented for peer review that is not consistent with the current paradigm will be rejected poste haste.

... snip ...

(emphasis added)

Really?

Do you happen to recall the two 'high-z' supernova teams (of astronomers), who published independent papers that (in effect) announced the discovery of 'dark energy'?

Do you happen to know what the (then) "current paradigm" was, in cosmology? (HINT: someone's 'greatest blunder')

Do you happen to know the names of the journals these teams' papers were published in, and whether they are peer-reviewed?

Have you heard of Halton Arp and/or Jayant Narlikar? of the 'variable mass hypothesis' that has their names associated with it (as in 'the Arp-Narlikar VMH')? Do you happen to know whether this VMH is "consistent with the current paradigm"? (HINT: it isn't) or where this was first published?

How many more examples like this do you need to be made aware of before you can appreciate just how silly (not to mention wrong) your statement is?

 

[Skwinty]

(emphasis added)

How many more examples like this do you need to be made aware of before you can appreciate just how silly (not to mention wrong) your statement is?

Correction. This was Witts statement not mine.
How can you say that Dark Energy is not consistent with the cosmological constant. Surely they are different interpretations of the same set of observations.

PS These individuals who wrote these papers were well known in Astronomy, they were not unknowns.

 

[godless dave]

Hi All
First of all I want to restate a few things again.
3. My questions and sometimes hostile statements come from the fact that the dismissing of Witt as a crank seems to be unfair.
He clearly states that he is presenting a philosophical theory that wants to get away from the standard model and then work towards a scientific theory.

6.Some of you may or may not buy his book for further investigation.
It is not fair to trash him based on the excerpts. But there again as he says, any theory presented for peer review that is not consistent with the current paradigm will be rejected poste haste.

The phrases I bolded are precisely what makes Witt a crank.

7. I dont have anything against the LHC or any scientific endeavours, merely some scepticism that these are going to produce the answers to everything or even most of every thing.

No one claims that it will! The LHC is being built to test certain hypotheses. How do you suggest we test hypotheses, by writing books and press releases?

8.As I said in a previous post, it seems as though the philosophy of science died with Einstein.

What do you mean by that? What approach did Einstein take that you think has been abandoned? Remember, Einstein wrote papers, including the math he did, and submitted them to the appropriate journals. They were published even though they weren't consistent with the current paradigm.

 

[Skwinty]

The phrases I bolded are precisely what makes Witt a crank.


No one claims that it will! The LHC is being built to test certain hypotheses. How do you suggest we test hypotheses, by writing books and press releases?



What do you mean by that? What approach did Einstein take that you think has been abandoned? Remember, Einstein wrote papers, including the math he did, and submitted them to the appropriate journals. They were published even though they weren't consistent with the current paradigm.

Witt is an unknown and his theory rejects the current paradigm in favour of his. The odds are totally against him regardless of the validity of his theory.

Back to the facetious one liners sigh

Einstein studied philosophy and his approach was philosophical.
Once again his theories were based on the current paradigm.
Newton , Maxwell , Mach , Bohr, Brown , de Broglie to name a few