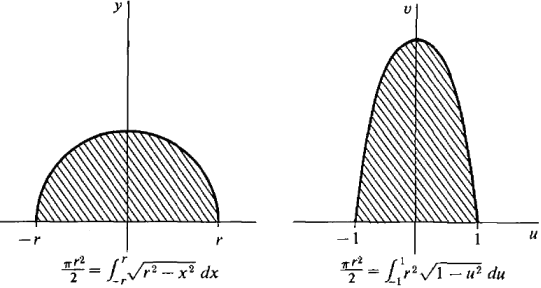Deeper than primes - Continuation

[doronshadmi]

Here is an example of verbal_symbolic AND visual_spatial pun:

It was taken from http://www-e.openu.ac.il/geninfor/openletter/ol18/pages12.pdf which researches brian's Glogal (non-local) Local linkage.

 

[doronshadmi]

By being aware of the non-locality of a line with respect to some point on it, it can be described as “curved” AND “straight” with respect to the point's domain, as shown in http://www.internationalskeptics.com/forums/showpost.php?p=7737500&postcount=114.

By understanding this fact it is realized that non-locality is the primary property of a line, where being “curved” OR “straight” is definitely secondary property of it.

Since verbal-only skill(ers) can't get the non-local primary property of a line (which can't be done without using also visual_spatial skills), they are wrongly defines a line by some secondary property of it (curvature, for example).

 

[jsfisher]

Lets put the maths to one side now and use pure thought.

Lets say we have an infinitely large circle, is the line around the edge of the circle curved or straight?

(a) Where would this circle be?
(b) Why do you assume curved and straight are mutually exclusive?

 

[epix]

Lets put the maths to one side now and use pure thought.

Lets say we have an infinitely large circle, is the line around the edge of the circle curved or straight?

Circles possess certain properties which they retain regardless of the their sizes. One of them is that to any point that lies on the circumference, a tangent line can be drawn. Since tangent line cannot be drawn to a straight line, the circumference of the circle must be always a curve for any radius larger than zero.

Now let's the "pure thought" deliver some hint. How do you draw one straight line? Here is an example: You make an initial point and drag your pencil in one direction - toward the east, for example. When you stop, one straight line is drawn. But when you start changing the direction of the straight line in the orthogonal manner (left, right, up, down), you draw a multitude of straight lines. Depending on you intention, the result may look like this:

Now think about it... "Is the line around the edge of the circle curved or straight?"

(Which one do you mean? There are many.)

 

[epix]

Since verbal-only skill(ers) can't get the non-local primary property of a line (which can't be done without using also visual_spatial skills), they are wrongly defines a line by some secondary property of it (curvature, for example).

Doron continuously takes issues with "traditional mathematics," and so it's safe to assume who the "verbal-only skill(ers)" may be.

Straight line:

"That which lies evenly between its extreme points."
~ Euclid ~

"The shortest line between two points."
~ Chauvenet ~

"A line which has the same direction through its whole length."
~ Newcomb ~

No mentioning of any curvature...

Doronetics and hostile-to-religion atheism were born in the same sewer where bubonic_plague_carrying_rats bit off the umbilical cords. Both disorders share the same pulpit to ooze their catechism from.

 

[doronshadmi]

Verbal_symbolic-only skill(ers) can get things only if they are packed in context-dependent frameworks.

From these fragmented boxes they can't comprehend the actuality of a one unified Cross-contexts AND Context-dependent framework, where Ethics AND Logic\Technological skills are organs of a one coherent organism.

In terms of Mathematics, the can't comprehend the difference between primary and secondary properties of a given form.

For example, if the considered form is a line, they get it only by its secondary properties, which are being curved OR straight.

By using also Cross-contexts knowledge of a line, its primary non-local property among its curved AND straight secondary properties (which are local w.r.t to the primary non-local property) is known, exactly as demonstrated, for example, by the following diagram:

The primary non-local property of a line w.r.t its curved AND straight secondary properties, is easily known, if one uses verbal_symbolic AND visual_spatial skills.

Verbal_symbolic-only skill(ers) get Ethics only if it is expressed by context-dependent frameworks, exactly as observed by the local-only view of different religions, cultures etc.

A one unified Cross-contexts AND Context-dependent framework, where Ethics AND Logic\Technological skills are organs of a one coherent realm, is exactly the framework that is developed beyond the current Context-dependent-only local-only view of different religions, cultures, logical\technological skills, etc.

 

[doronshadmi]

Being curved or straight is mutually exclusive (local and secondary property) w.r.t the non-local primary property of a form like a line, where by the non-local primary property of a line can be curved AND straight.

The following diagram clearly demonstrates the primary\secondary properties as a one comprehensive framework:

 

[punshhh]

Circles possess certain properties which they retain regardless of the their sizes. One of them is that to any point that lies on the circumference, a tangent line can be drawn. Since tangent line cannot be drawn to a straight line, the circumference of the circle must be always a curve for any radius larger than zero.

Now let's the "pure thought" deliver some hint. How do you draw one straight line? Here is an example: You make an initial point and drag your pencil in one direction - toward the east, for example. When you stop, one straight line is drawn. But when you start changing the direction of the straight line in the orthogonal manner (left, right, up, down), you draw a multitude of straight lines. Depending on you intention, the result may look like this:

[qimg]http://ciks.cbt.nist.gov/garbocz/paper32/fig1.gif[/qimg]

Now think about it... "Is the line around the edge of the circle curved or straight?"

(Which one do you mean? There are many.)

Thankyou Epix,
So the line around the edge of a circle is an infinite number of infinitely short straight lines arranged as a zigzag. Or perhaps an infinite number of tangents/facets?

Is this also the case for an infinitely large circle?

 

[punshhh]

(a) Where would this circle be?
(b) Why do you assume curved and straight are mutually exclusive?

(a) in a hypothetical unlimited space, 2 or 3 dimensions.

(b) one is straight and the other is curved, unless you can explain how one can be the other?

 

[doronshadmi]

Thankyou Epix,
So the line around the edge of a circle is an infinite number of infinitely short straight lines arranged as a zigzag. Or perhaps an infinite number of tangents/facets?

Is this also the case for an infinitely large circle?

punshhh, please be aware of the fact that if the circumference has zigzag shape, pi is not an invariant value, or in other words, the considered form is not a circle.

 

[jsfisher]

(a) in a hypothetical unlimited space, 2 or 3 dimensions.

Yes, but where? Let's say for the sake of discussion the circle's center is at the origin. Now, can you tell me where any point on the circle is located? If you'd prefer, put the center somewhere else of your choosing, then locate any point on the circle.

(b) one is straight and the other is curved, unless you can explain how one can be the other?

You are substituting colloquial meanings of words for the more precise meanings used in Mathematics. That is acceptable to a point, because it can certainly facilitate communication were the nit-picky details and qualifications are understood. On the other hand, when it is used as Doron does, to confuse and obfuscate the nit-picky details and qualifications -- in effect to disprove a definition -- then it is totally unacceptable.

In Mathematics, straight is a special case of curved, not an alternative. Curves include the straight lines.

Doron's disagreement with this is strictly to just disagree; he has no salient point.

 

[epix]

Thankyou Epix,
So the line around the edge of a circle is an infinite number of infinitely short straight lines arranged as a zigzag. Or perhaps an infinite number of tangents/facets?

Is this also the case for an infinitely large circle?

Essentially yes. It is the task that defines an objects. Calculus sees curves as a collection of straight lines. In other words, any curve segment is made of infinitely many straight lines, like in this semicircle:

You can see now that it's easy to compute the area of the semicircle by computing the area of each rectangle and by adding them together - there are infinitely many of them though, but the technique of integration can handle the task:

 

[The Man]

Its all about spinning, the greater the curvature the faster the spin.

When it reaches a point you will be spinning at an infinite rate.

If by spinning you mean angular velocity, then a smaller diameter disc (more curved) would have to have a greater angular speed (RPM) to obtain the same tangential speed as a larger diameter (less curved) disc. What “point” “will be spinning at an infinite rate” and when do you ’reach’ it?

If by spinning you mean twisting words and phrases to suit ones needs then I seriously doubt Doron could be spinning any faster.

 

[doronshadmi]

By verbal_symbolic-only Mathematics, secondary properties like straight or curved block the ability to get the primary non-local property of, for example, a line.

More details about this fine subject are found in:

http://www.internationalskeptics.com/forums/showpost.php?p=7744169&postcount=126

http://www.internationalskeptics.com/forums/showpost.php?p=7744317&postcount=127

punshhh, verbal_symbolic-only skill(ers) can offer you only "packed in boxes" Mathematics, that has no ability to get things also beyond their context-dependent restrictions.

More you communicate with them more you realize how they simply can't get Mathematics in terms of verbal_symbolic AND visual_spatial skills as a one comprehensive framework.

 

[punshhh]

If by spinning you mean angular velocity, then a smaller diameter disc (more curved) would have to have a greater angular speed (RPM) to obtain the same tangential speed as a larger diameter (less curved) disc. What “point” “will be spinning at an infinite rate” and when do you ’reach’ it?

A true point and you can't reach it. Can you imaging a spin of infinite rate?
Can it be represented mathematically?

 

[epix]

A true point and you can't reach it. Can you imaging a spin of infinite rate?
Can it be represented mathematically?

It can be imagined physically using Einstein's theory of relativity. In other words, a physical object cannot exceed the speed of light - there is no source of energy to make it happen. So your scenario wouldn't materialize.

In purely abstract, non-physical sense, anything can be infinitely accelerating, even a bowl of mashed potatoes.

 

[epix]

punshhh, verbal_symbolic-only skill(ers) can offer you only "packed in boxes" Mathematics, that has no ability to get things also beyond their context-dependent restrictions.

More you communicate with them more you realize how they simply can't get Mathematics in terms of verbal_symbolic AND visual_spatial skills as a one comprehensive framework.

Punshhh, Doron has only two pics of his own that he keeps exhibiting (Doronian side-orders). Otherwise his sermon is the "verbal_symbolic_only" style that he finds alone insufficient to understand the depths of mathematics doronized beyond recognition.

 

[The Man]

A true point and you can't reach it. Can you imaging a spin of infinite rate?
Can it be represented mathematically?

"A true point"? Well a mathematical point has no dimensions (thus no spinning) itself. A spin rate (as angular change per unit time) requires two dimensions, angle and time. Can you imagine a spin of zero rate? It can be represented mathematically; 0 change in angle (since a point has no angle, circumference, diameter or any other dimensional attribute itself), we can even represent that lack of anglular change for a mathematical point in radians (a dimensionless quantity), over X seconds (wait as long as you want the non-dimensionality of a mathematical point wont change), gives a rate of 0 radians /X seconds =0 radians/ second. The only real difference is that we are now considering a different point in time as time is a dimension, so the point of contention would still be back at that original time no matter how much one might like to just “spin” it into the future.

 

[epix]

"A true point"? Well a mathematical point has no dimensions (thus no spinning) itself. A spin rate (as angular change per unit time) requires two dimensions, angle and time. Can you imagine a spin of zero rate? It can be represented mathematically; 0 change in angle (since a point has no angle, circumference, diameter or any other dimensional attribute itself), we can even represent that lack of anglular change for a mathematical point in radians (a dimensionless quantity), over X seconds (wait as long as you want the non-dimensionality of a mathematical point wont change), gives a rate of 0 radians /X seconds =0 radians/ second. The only real difference is that we are now considering a different point in time as time is a dimension, so the point of contention would still be back at that original time no matter how much one might like to just “spin” it into the future.

Punshhh lives in rural England and that affects his questions regarding objects that move "infinitely fast." People who live on the farm sometimes share their experience with others regarding the phenomenon where they moved infinitely fast when the friction forces didn't work for them and the ladder that they must often climb started to slip beneath them.

A ladder leans against a wall. It begins to slide, the top end moving down the wall and the bottom end across the floor away from the wall.

Such a scenario is the basis for a variety of calculus problems. For example, if the ladder's bottom end moves away from the wall at a constant speed, what is the velocity of the top of the ladder at any given instant? Curiously, the mathematical model indicates that the velocity of the top approaches infinity when the ladder hits the floor.

Aaah, those symbolic_verbal_only skill(ers)! They can't get anything right.

http://www.maa.org/mathtourist/mathtourist_11_11_08.html

 

[The Man]

Punshhh lives in rural England and that affects his questions regarding objects that move "infinitely fast." People who live on the farm sometimes share their experience with others regarding the phenomenon where they moved infinitely fast when the friction forces didn't work for them and the ladder that they must often climb started to slip beneath them.

Aaah, those symbolic_verbal_only skill(ers)! They can't get anything right.

http://www.maa.org/mathtourist/mathtourist_11_11_08.html

Well, I live in rural New York, though I did have to study mechanics of materials (compression, elongation, stress, strain and such physical attributes that you allude to) before I was employed as a mechanical engineer.