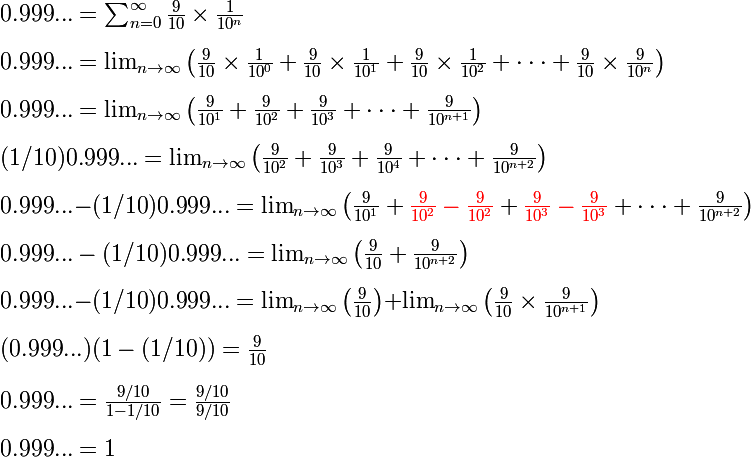
Let's correct what I wrote in
http://www.internationalskeptics.com/forums/showpost.php?p=10305716&postcount=4275.
The right one is this:
--------------------------------------
By using |
R| size observation:
0.999...
10 < 1 by 0.000...1
10
0.888...
9 < 1 by 0.000...1
9
The difference between 0.000...1
10 and 0.000...1
9 is given by direct proportionality, according to the following formula:
abs( (1/9)/(1/10) ) (the result can't be expressed by any particular base, because this ratio is done between bases).
The general formula for all
n>1 natural numbers is:
base j = 2 to
n
base k = 2 to
n
abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k.