doronshadmi
Penultimate Amazing
- Joined
- Mar 15, 2008
- Messages
- 13,320
Dear Apathia,
First of all thank you for your open heart AND reasoning, which enables you to know that the non-composed hugging hands is not a collection of the hugged
The attempt to define the non-composed in terms of its finitely or infinitely many expressions (in terms of the composed) creates the paradox.
The paradox is solved by being aware of the following hierarchy of existence:
1. Actual infinity existence (the non-composed).
2. The finitely weaker exitance w.r.t (1) (the finitely composed expression of (1), which is not the non-composed).
3. The infinitely weaker exitance w.r.t (1) (the infinitely composed expression of (1), which is not the non-composed).
So dear Apathia, we do not use two baskets in order to solve the paradox, because by doing so, we are still closed under the exitance of being composed.
Actual infinity existence (the non-composed) is not one-of-many existence (its existence is defined in terms of quality).
Its qualitative existence is defined, whether it weakens itself in order to expresses itself in terms of the composed (each expression is defined in terms of one-of-many finitely or infinitely many things (its existence is defined in terms of quantity), or not.
Please observe the following diagram by using visual_spatial AND verbal symbolic reasoning:
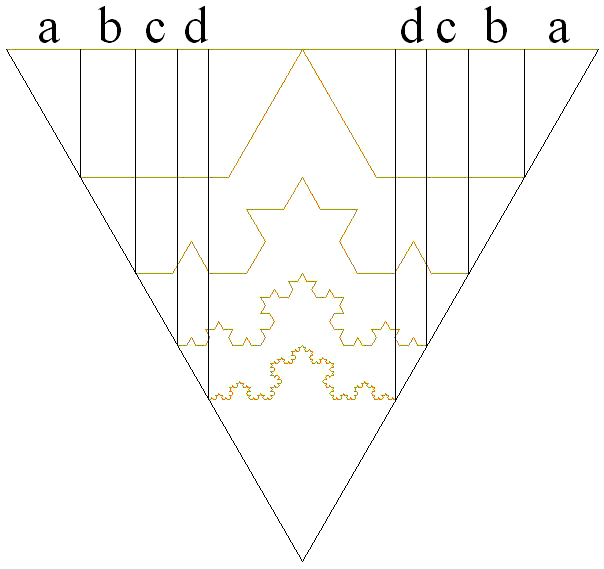
What we observe is ______ (non-composed object) that its bent forms (where being bent does not change the fact that each bent form is actually non-composed) are reflected as marks along it, such that the non-finite series 2(a+b+c+d+...) (which is a composed form) is infinitely weaker than the non-composed property of ______
As a result 2(a+b+c+d+...) < some fixed (or accurate) quantitative value that was given to the non-composed quality of _______ (where infinitely many reflected non-composed bent forms with the same fixed (or accurate) quantitative value, actually define the series 2(a+b+c+d+...) such that it is < the given fixed (or accurate) quantitative value, exactly because of the inability to define the quality of ______ by quantitative values).
As a result, there is an endlessly smaller ___ as the complement of 2(a+b+c+d+...) to the quantitative accurate value that was given to ______ (where this complement quantitative value is endlessly changing (its fixed (or accurate) quantitative value, can't be defined)).
First of all thank you for your open heart AND reasoning, which enables you to know that the non-composed hugging hands is not a collection of the hugged

Apathia said:Collapsing the baskets into one creates the paradox
The attempt to define the non-composed in terms of its finitely or infinitely many expressions (in terms of the composed) creates the paradox.
The paradox is solved by being aware of the following hierarchy of existence:
1. Actual infinity existence (the non-composed).
2. The finitely weaker exitance w.r.t (1) (the finitely composed expression of (1), which is not the non-composed).
3. The infinitely weaker exitance w.r.t (1) (the infinitely composed expression of (1), which is not the non-composed).
Apathia said:"The Barber shaves" goes into one basket, and the "only those men in town who don't shave themselves" into another basket.
So dear Apathia, we do not use two baskets in order to solve the paradox, because by doing so, we are still closed under the exitance of being composed.
Actual infinity existence (the non-composed) is not one-of-many existence (its existence is defined in terms of quality).
Its qualitative existence is defined, whether it weakens itself in order to expresses itself in terms of the composed (each expression is defined in terms of one-of-many finitely or infinitely many things (its existence is defined in terms of quantity), or not.
Please observe the following diagram by using visual_spatial AND verbal symbolic reasoning:

What we observe is ______ (non-composed object) that its bent forms (where being bent does not change the fact that each bent form is actually non-composed) are reflected as marks along it, such that the non-finite series 2(a+b+c+d+...) (which is a composed form) is infinitely weaker than the non-composed property of ______
As a result 2(a+b+c+d+...) < some fixed (or accurate) quantitative value that was given to the non-composed quality of _______ (where infinitely many reflected non-composed bent forms with the same fixed (or accurate) quantitative value, actually define the series 2(a+b+c+d+...) such that it is < the given fixed (or accurate) quantitative value, exactly because of the inability to define the quality of ______ by quantitative values).
As a result, there is an endlessly smaller ___ as the complement of 2(a+b+c+d+...) to the quantitative accurate value that was given to ______ (where this complement quantitative value is endlessly changing (its fixed (or accurate) quantitative value, can't be defined)).
Last edited:

