Cherepanov's "fracture wave" theory

[rwguinn]

Since the Cherepanov paper is quite obviously ridiculous (it is based on the application of a demolition wave equation to etched glass), I am going back to the related topic: B&Z 2002.



Any plastic deformation, whether it represents a "complete buckle" or not, absorbs energy and should be included in a proper Wp calculation.



You mean: all 80 some floors do not contribute to We.

In a simple one-dimensional analysis, which is what Bazant limits himself to, they certainly do.

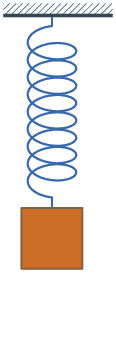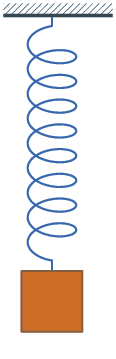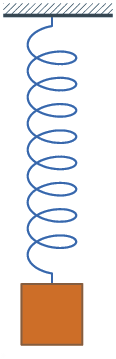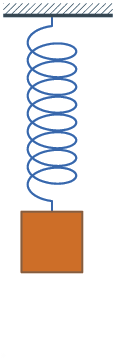
A long spring can elastically absorb more energy in compression than a short one, just like the fact that you can strench a longer rubber band farther than a short one before it breaks. Elastic energy is dispersed across all the atomic bonds, not just a few of them.

This is my last reponse to you, buit because it is important, I'm going to respond on this one.
The 80-odd floors are NOT a "Long Spring". They form 80-odd SHORT springs. For the appropriate analogy, take your rubber band and tie lots of short rubberbands to it at regular intervals, then tie the short ones to ground at their other end.

 

[cmcaulif]

plastic deformation below the crushing front in the B&V model is highly unlikely, a column cant transmit a load larger than it can bear itself.

I have no idea why you think 80 floors would act as ONE spring by the way, plenty on that in this thread especially the appendices.

 

[bofors]

The 80-odd floors are NOT a "Long Spring". They form 80-odd SHORT springs.

Come on now, this is basic physics.

One 80-floor spring or 80 one-floor springs, it makes no differnce, my point still stands.

See how the entire springs contracts (not just the part of it near the mass block):

 

[cmcaulif]

there is already a thread, which YOU started, for discussing B&Z by the way

 

[bofors]

plastic deformation below the crushing front in the B&V model is highly unlikely...

Sure... but the exact length of the crushing front would is an important question, something Bazant seems to ignore (or rather just assumes is a floor or two).

...a column cant transmit a load larger than it can bear itself.

Sure... but that does not mean that no energy is elastically transferred either. Basically, the amount of energy that can be transferred elastically is transferred elastically. This is not zero as Bazant proposes and under his simple (and absurd) impact model, the amount of energy that can be transferred in elastically is 100%. See B&Z 2002, pape 2, Figure 2(a).

I have no idea why you think 80 floors would act as ONE spring by the way, plenty on that in this thread especially the appendices.

Thanks for reference, I will look at the thread and hopefully find the appendices.

 

[cmcaulif]

the lenght of the crushing front will be short because as I said, a column can't transmit a load larger than it can bear itself. In order for 'crushing' to occur you need plastic deformation. If you have a column with a Pcr of X on top of a column with a Pcr of X+A, the column on top will fail first.

Sure... but that does not mean that no energy is elastically transferred either. Basically, the amoung of energy that can be transferred elastically is transferred elastically. This is not zero as Bazant proposes and under his simple (and absurd) impact model, the amount of energy that can be transferred in elastically is 100%. See B&Z 2002, pape 2, Figure 2(a).

I never said that no elastic deformation would occur, I said plastic deformation is unlikely, then I linked you to a post, with links in the op which calculates the elastic deformation below the crushing front.

FFS, it helps to read what I post don't you think?

 

[bofors]

... then I linked you to a post, with links in the op which calculates the elastic deformation below the crushing front.

I am looking at Newton Bit's work now, thank you.

 

[Dave Rogers]

A proper analysis would consider elastic (We) and plastic (Wp) dissipation in relation to the potential energy (Wg).

Basically, Bazant seems to be arguing that:

Wg >> (We + Wp)

Actually, I'd question that, although the engineers round here may be able to set me straight. Consider the sequence:

1) Initial impact. All the energy is kinetic, equal to Wg.
2) Elastic compression phase. Elastic energy increases to We, kinetic decreases to Wg-We. If Wg>We, we have progression to:
3) Plastic deformation phase. This progresses to the failure point, where plastic deformation energy is Wp. Kinetic energy is now Wg-We-Wp.

The failed columns have now fractured, so can not be under elastic strain. The total energy of the system is therefore the sum of kinetic + plastic, i.e. E(total) = Wg-We-Wp+Wp = Wg-We.

Where did We go? (Wrong?)

Doesn't the elastic energy dissipate into the plastic deformation phase as the failing columns unload, hence effectively being recovered and reducing the energy requirement to Wg > MAX(We, Wp) ?

Dave

 

[einsteen]

Come on now, this is basic physics.

One 80-floor spring or 80 one-floor springs, it makes no differnce, my point still stands.

See how the entire springs contracts (not just the part of it near the mass block):

I agree that one spring can be thought of as connected sub-springs. But the problem is that we have 110 point masses in this model. That makes it different, in two springs the force balance out very quickly but with a mass between it is different. In order to prove global collapse one should setup a model with n springs falling on 110-n springs, but not real springs but springs that have the property they are elastic (kx) at a small range in the beginning for example, then a plastic range and then a drop-down.

The "'springs" should become stronger when you go to the bottom, which implies that those of the impacting top section are weaker, but then the mass distribution is also highly relevant. Although the solution might be impossible to find the collapse could be substituted into it in order to check if it fits the equations. Major job.