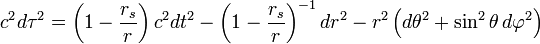I have to go, and will catch up later, but very briefly, this one is hugely important:
I'm not kidding about this. There is no "time flowing" in the NIST caesium fountain clock. Just electromagnetic hyperfine spin flips occurring and microwaves moving. I would urge you to look into this, it's probably about the most important thing there is. That and the parallel-mirror light clock that runs slower at the lower elevation. Again there's no time flowing in it, just light moving.
We define the second using the hyperfine transition and microwaves. These microwaves only have a defined frequency after we've defined the second. To do that we count 9 192 631 770 microwaves into the detector and then say a second has elapsed. When the microwaves are moving slower, the second is bigger. Then we use it and the motion of light to define the metre. (This doesn't change because the slower light and the bigger second cancel each other out). Then we use the speed of light to measure the speed of those microwaves.DeiRenDopa said:But I can't see how he can possibly be right re the second (the unit of time), even allowing for sloppy language.
I'm not kidding about this. There is no "time flowing" in the NIST caesium fountain clock. Just electromagnetic hyperfine spin flips occurring and microwaves moving. I would urge you to look into this, it's probably about the most important thing there is. That and the parallel-mirror light clock that runs slower at the lower elevation. Again there's no time flowing in it, just light moving.