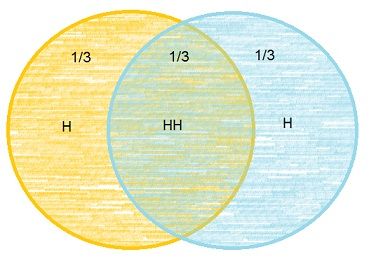
First coin or last coin is arbitrary and of no consequence as it’s not defined as a double coin toss. It’s two single and independent coin tosses that each have odds of 1/2. That one independent coin toss ended up being heads doesn’t affect the odds of the other independent coin toss. Each independent coin toss is ether H or T with equal odds.Are you saying there's no difference between "at least one of the two coins landed heads" and "the first coin landed heads"?
As I see it, "at least one of the two coins landed heads" is equivalent to: (HH or HT or TH).
And "the first coin landed heads" is equivalent to: (HH or HT).
"At least one of the two coins landed heads" is equivalent to: (H or T) and H was the result.