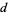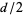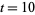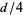Infinitesimals and calculus

[IllegalArgument]

Interesting, I was taught epsilon, delta in simplified form in Freshman calculus and then learned it from the ground up in Real Analysis as a grad student. I was required to take Real Analysis because the formal math used for Measure Theory and most of System Theory requires a good foundation of limits, convergence and set theory, all of which you will get in a good Real Analysis course. That is a senior level undergrad math course that anyone wanting a BS in math must take at UT. It was a hard course but it was worth the effort. It clarified a lot of things that were glossed over in my other math courses.

I look forward to learning set theory. I'm a self taught programmer, with giant holes in my formal education. Trying to fill them in starting with calculus.

 

[wrs]

If I am not mistaken, Newton developed calculus without the concept of limit -- that came later. In Fluxional Calculus he used more or less the same hack.

Newton developed the ideas behind calculus but he didn't develop the depth of understanding of the subject that we have today. Calculus was not born fully developed, no system of knowledge ever is. The derivative is a Linear Operator but that idea didn't exist when Newton started thinking about them. To me the epsilon delta approach encompasses the higher notions better than does infinitesimals.

 

[Anerystos]

Some nothings are bigger than other nothings. It all depends where you got them from.

 

[Soapy Sam]

Some nothings are bigger than other nothings. It all depends where you got them from.

That's exactly the sort of thing math teachers should not say, because in English, it's nonsense and you are teaching people who know English ( or other language) but don't know how nothings can differ.

Another example is root of minus 1. I was clearly told in school that any number, squared ,gives a positive answer. That clearly means (in English) that the square root of a negative number is a nonsensical concept. So imaginaries came as a shock.

Teachers have to be careful what they say, in case they are believed and that belief sets future limits to understanding. Hard job, teaching.

 

[jsfisher]

That's exactly the sort of thing math teachers should not say, because in English, it's nonsense and you are teaching people who know English ( or other language) but don't know how nothings can differ.

Another example is root of minus 1. I was clearly told in school that any number, squared ,gives a positive answer. That clearly means (in English) that the square root of a negative number is a nonsensical concept. So imaginaries came as a shock.

Teachers have to be careful what they say, in case they are believed and that belief sets future limits to understanding. Hard job, teaching.

Aren't many subjects taught that way, as a sequence of refinements to the "truth"? The square root of a negative number may well be a nonsensical concept, but then, too, at some period in each of our lives, negative numbers itself was a nonsensical concept.

As for infinitesimals vs. limits. Meh. Limits are more rigorous, but infinitesimals are simpler conceptually and more direct for getting at the slope and area concepts of Calculus.

Were I teaching Calculus, I think I'd probably speak in terms limits, but rely on infinitesimal concepts to side-step the horrors of Mr. Delta and Mr. Epsilon.

 

[wrs]

Some nothings are bigger than other nothings. It all depends where you got them from.

Some infinities are countable, others are not.

 

[Chris Haynes]

Here's an book from 1912, Calculus made easy.

It shows how to calculate a few basic derivatives w/o mentioning limits.

http://www.gutenberg.org/files/33283/33283-pdf.pdf

That looked familiar. So I went to the pile of stuff left in my house by my son who is a math major, and saw the small 1957 edition of that book. I had seen it, but never looked inside.

It is adorable, and quite funny. I like how he introduces the first chapter as being about the "first terror."

 

[lenny]

Math gets more and more abstract when it's actually applied to real world problems. .

Great observation!

Often the motivation for action just gets more and more arbitrary: as the ends attempt to justify them means. That's not really maths, but common in physics. Usually physicists just plunge ahead, sometimes the mathematicians make sense of it later, other times the mathematical justification remains missing, so far...

 

[Soapy Sam]

Some infinities are countable, others are not.

Getting OT here, but if a number is not countable, what actual properties does it have?

 

[jsfisher]

Getting OT here, but if a number is not countable, what actual properties does it have?

Oh, the possibilities would be infinite....


Sorry. Couldn't resist. I'll get me coat....

 

[wrs]

Getting OT here, but if a number is not countable, what actual properties does it have?

Infinity isn't a number, it just means something without limit. A countably infinite set A is defined to be any set on which there exists a one to one and onto function that maps the elements of a A to the set of Natural Numbers. The set of integers is countably infinite for example. The simpler concept is that you can enumerate all the entities in the set even though it might take forever. So a countable infinity would correspond to the number of elements in a countably infinite set. An uncountable infinity would be the number of elements in the set R of real numbers.

 

[marplots]

Getting OT here, but if a number is not countable, what actual properties does it have?

It might be larger or smaller than something else. It might be divisible by two or it might be prime. And it might be blue.

 

[Chris Haynes]

Getting OT here, but if a number is not countable, what actual properties does it have?

And they can be useful if you don't stare too much at your navel contemplating the wonders of teeny tiny and incredibly big... there are limits. Literally.

Take this joke that is related in MathWorld's entry for Zeno's Paradoxes:

The dichotomy paradox leads to the following mathematical joke. A mathematician, a physicist and an engineer were asked to answer the following question. A group of boys are lined up on one wall of a dance hall, and an equal number of girls are lined up on the opposite wall. Both groups are then instructed to advance toward each other by one quarter the distance separating them every ten seconds (i.e., if they are distance

apart at time 0, they are

at

,

at

,

at

, and so on.) When do they meet at the center of the dance hall? The mathematician said they would never actually meet because the series is infinite. The physicist said they would meet when time equals infinity. The engineer said that within one minute they would be close enough for all practical purposes.