Richard Gage Blueprint for Truth Rebuttals on YouTube by Chris Mohr

[R.Mackey]

"Margin of error" is a decisional estimate. We speak in terms of "margin" in engineering when we are trying to quantify validity of a determination against uncertainty. For instance, "this ship will not capsize," with a margin of error of 100 tons, means that to the best of our knowledge it can handle approximately 100 tons more cargo / passengers / bilge before it becomes unstable.

This is different than the more relevant "measurement uncertainty." All measurements have uncertainties due to random error, sampling error, experimental error, systematic error. Good researchers try to quantify this error, but in most situations this error is assumed to be quasi-Gaussian, and therefore symmetric. So we might say "the measured rate of descent of WTC 7 was 9.6 m/s² +/- 1.0," where 1.0 m/s² is the error estimate. (These are made-up numbers for purpose of discussion.) Unless stated otherwise, this error estimate corresponds to a one-sigma error bound, i.e. we are roughly 68% confident that the real value lies within one interval of our estimate.

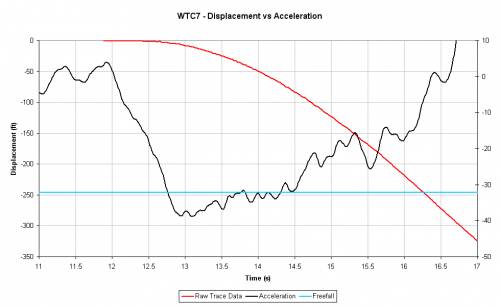
Using the above measurement, we might say "WTC 7 descended slower than Free-Fall Acceleration," viz., it descended at less than g with 0.2 m/s² to spare. This 0.2 m/s² is the "margin of error," i.e., if we exceed this margin, our declaration is wrong.

Now in this fake example, note that the "margin of error" is much less than the error estimate. So, in this case, we really have no "margin of error." Our declaration is very unreliable.

On the other hand, suppose we measured the rate of descent to be 6.5 m/s² +/- 1.5. In this case, we would have a margin of about 3.3 m/s², which is reasonably large compared to the error estimate. In this case, we have a comfortable, but not bulletproof, margin for error in making our declaration.

Hope that helps. Let us all strive to avoid semantic arguments.

 

[Dave Rogers]

I'm still not clear why I'm misusing the term margin-of-error. Maybe femr can help. In my mind, let's just say femr puts out some measurements and says, these are accurate to within +/- 0.06%, meaning that in addition to calculating his data, he has also calculated how far off that data may be due to camera movement, heat waves in the air, and the limits of sub-pixel resolution. Is that correct? Why does the term margin of error NOT describe such a qualifier? Am I just using the wrong term or am I still missing a central concept here?

The nearest you're getting to any kind of misuse of the term is that "margin of error" is more commonly used in statistical sampling, whereas scientists and engineers talk about measurement error or observational error. I think femr2's whole "if you choose to specify margin of error in this context" bit is to try and pretend he didn't make a stupid and embarrassing error; I've never heard of any other definition of "margin of error" that has the mathematical properties his ">0" answer implies.

Of course the reason I am asking this is because of the question of possible >g collapse of part of the north perimeter wall. From the NIST data alone, because they never gave a "margin of error" or whatever (and because their techniques of measurement were less precise), it seems that my statement "maybe greater than freefall acceleration" is all I can say. femr's data, which is more accurate, can show that >g acceleration did happen, and based on that data I don't even need the qualifier "maybe." Is this correct?

Yes. If you accept femr2's data - and it seems reasonable to me to do so - then it follows inevitably is reasonable to conclude [1] that the period of >g acceleration is real.

Dave

[1] Revised because R. Mackey's rather more rigorous treatment is of course correct.

 

[femr2]

I'm still not clear why I'm misusing the term margin-of-error.

I think the only issue is stating that when all values are within "margin of error" that AT FFA is valid. In reality each value could actually be anywhere within the range, and none of it at all may be AT FFA.

Margin of Error is a more stats based phrase. Uncertainty would be more appropriate I think...but it doesn't really matter too much imo. Everyone knows what is intended here I think.

let's just say femr puts out some measurements and says, these are accurate to within +/- 0.06%, meaning that in addition to calculating his data, he has also calculated how far off that data may be due to camera movement, heat waves in the air, and the limits of sub-pixel resolution. Is that correct?

I would be unlikely to suggest a percentage (as that has scaling issues) but sure. There are formal methods for determining uncertainty, though I personally see no issue with variance based estimates.

Of course the reason I am asking this is because of the question of possible >g collapse of part of the north perimeter wall. From the NIST data alone, because they never gave a "margin of error" or whatever (and because their techniques of measurement were less precise), it seems that my statement "maybe greater than freefall acceleration" is all I can say. femr's data, which is more accurate, can show that >g acceleration did happen, and based on that data I don't even need the qualifier "maybe." Is this correct?

I'm confident that the general shape of the acceleration graph is true.

The same general profile shape emerges from multiple datasets and multiple viewpoints when acceleration is derived.

I'm confident that the magnitude of the profile is derived from data which has been handled as carefully as possible, with the most accurate building metrics available for translation between pixel units and real-world units.

Similar magnitude also emerges from the various datasets I've generated.


The very simplest of descent traces indicate ~FFA. My data ALSO indicates a period of ~FFA, but with the addition of a short period >g.

It can be easily seen why that period occurs if you compare the NIST linear fit to my own velocity data..


In simplistic terms, to get the velocity back onto the ~FFA line, there HAS to be a brief period of >g between around 12-13.5s.

If you're confident that ~FFA is reached via the other datasets (NIST & Chandler) then I suggest confidence in the NW corner data provided by myself, including over-g period.

NW Corner. An important point. Not the entire building.


ALSO...if it is of note to you...

...the NIST formula for velocity (if derived for acceleration (which NIST didn't bother to do)) also includes a period of over-g behaviour (for their "position" along the roofline, not the NW corner).

I think there is little doubt that brief moments of >g were experienced by multiple locations along the North Facade of WTC7 early in descent.

 

[MarkLindeman]

I'm still not clear why I'm misusing the term margin-of-error. Maybe femr can help. In my mind, let's just say femr puts out some measurements and says, these are accurate to within +/- 0.06%, meaning that in addition to calculating his data, he has also calculated how far off that data may be due to camera movement, heat waves in the air, and the limits of sub-pixel resolution. Is that correct? Why does the term margin of error NOT describe such a qualifier? Am I just using the wrong term or am I still missing a central concept here?

In addition to other good posts --

Chris, I have two reservations about your statement that "using the NIST graph, the measurements show FFA within the margin of error" (apart from the fact that we don't actually know the "margin of error"). Neither one of them entails that you are misusing margin of error, per se. Ordinarily I try to avoid raising semantic objections, but this entire argument with c7 hinges on semantic equivocations, so I want to make sure that we're all on roughly the same page.

It's true that for any estimate of average acceleration over some period of time, we should be able to calculate a margin of error, and see whether FFA is within that margin of error or not. Ryan's post elaborates on this point. (Interestingly, the most common ways to calculate a "standard error" and thus a "margin of error" for the slope don't use any information about possible errors in the measurements. If you fit a line to two points, the standard error will always be zero: the line fits perfectly!)

One reservation is that "show FFA within the margin of error" seems to imply that FFA is the Right Answer. At most one could infer that FFA might be the Right Answer -- well, a bit more than that: that we think the Right Answer is close to FFA.

The second reservation is: if FFA is or might be or is close to the Right Answer, what was the question? Was g the average acceleration over some period, or was it the constant acceleration over some period? c7 has backed down some, but for the most part he seems to have argued either that g is the constant acceleration, or in the alternative, that it is mere "verbiage" to care about the distinction. Since c7 apparently believes that "FFA proves CD," I sort of understand his point of view. But if we're going to have an intelligible discussion, we can't very well rule out distinctions between averages and constants.

 

[femr2]

The nearest you're getting to any kind of misuse of the term is that "margin of error" is more commonly used in statistical sampling

Aye. As I said uncertainty is probably the right term.

I think femr2's whole "if you choose to specify margin of error in this context" bit is to try and pretend he didn't make a stupid and embarrassing error; I've never heard of any other definition of "margin of error" that has the mathematical properties his ">0" answer implies.

>0 ... any "margin of error". As I said before...

I don't really think he should be talking about..."margin of error"...at all, but sure, if you choose to specify margin of error in this context. Perhaps tfk will turn up and bore everyone silly with protracted discussion of enourmous levels of uncertainty using the most long-winded notation possible.

Of course, in the context of the data being discussed, and any non-zero "margin of error", it is still impossible to say if any particular value is a particular exact value.

Yes. If you accept femr2's data - and it seems reasonable to me to do so - then it is reasonable to conclude that the period of >g acceleration is real.

Splendid.

 

[chrismohr]

Thanks all. BTW I'm starting another round of the www.chrismohr911.com debate with Gage and friends based on my YouTubes. I have redone some of the stuff in reasons 1-13. Do watch the videos if possible to get the context before looking at all this.

 

[Christopher7]

OK I'm still wrapping my mind around my "margin of error" question. Sorry I am so slow here. It looked to me that NIST took their measurements (femr says they were entered by hand, but by whatever method they took raw measurements from a video) and entered them on a graph as a series of dots. In Phase Two, they then plotted a straight line representing freefall acceleration and showed that all of the dots they plotted were very close to that freefall line, some very slightly above and some very slightly below. The average of those dots comes to freefall. Am I right so far?

The software draws the line.

Now let's go to Mark Lindeman's post and my response at the top of this page, where he talks about an "error bar," which to my knowledge does not exist in any of NIST's, femr's or Chandler's graphs.

That's right. He made that term up. It's bombastic obfuscation verbiage.

If it did, however, in the NIST Report, I would think that error bar would be an equal area on both sides

No, the data points [dots] are inaccurate due to the fact they are taken from a video. Some are more inaccurate than others. That's why the program has a feature that computes the average and draws the line.

Any mistake I am making in understanding here pales in comparison to Chris7,

No, you are promoting pseudo-science from highly biased anonymous posters on a highly biased forum to refute real science. I am criticizing you for doing so.

whose repeated attacks against me include this false assertion: "You claim that NIST and Chandler don't know what they are talking about and the posters here know better. You claim the the programs they used, that were designed to measure velocity and acceleration, are wrong and the posters here know better." Please show me where I said NIST and Chandlere do not know what they are talking about and I will apologize and retract that statement. If you cannot find a quote where I said this, please retract your assertion and apologize to me. Stop being such a jerk.

You did not use those words but your saying/implying they are wrong is effectively the same thing. I will look for quotes this evening.

NIST and Chandler know what they are talking about. They used an accepted scientific method to determine FFA. There is no need for more or more accurate data or they would have done so.

FEMR's velocity graph confirms their findings of ~2.25 to 2.5s of FFA.

 

[femr2]

The software draws the line.

What software is that ? Draws the line ? Jebus.

He made that term up.

Incorrect.

No, the data points [dots] are inaccurate due to the fact they are taken from a video. Some are more inaccurate than others. That's why the program has a feature that computes the average and draws the line.

What software is that ?

And..."the AVERAGE"...finally.

NIST and Chandler know what they are talking about.

YOU don't even seem capable of correctly understanding what they are talking about, regardless of whether they do or not. Not a good starting position.

They used an accepted scientific method to determine FFA.

Which was ? And ... ~FFA, ffs. AVERAGE. APPROXIMATE.

FEMR's velocity graph confirms their findings of ~2.25 to 2.5s of FFA.

Again, no, it does not. Yet again you show your utter inability to interpret data correctly. Stop deliberately and willfully citing dumb-ass values you pluck from your derrier and attribute to my data.

Quite why I am still wasting any time with you is beyond me.

Given the hand-holding you have had there is absolutely NO WAY that you don't KNOW you are talking crap.

Tell you what, I'll see if I can get David to drop by the911forum, help you out like

 

[LSSBB]

What software is that ? Draws the line ? Jebus.


Incorrect.


What software is that ?

And..."the AVERAGE"...finally.


YOU don't even seem capable of correctly understanding what they are talking about, regardless of whether they do or not. Not a good starting position.


Which was ? And ... ~FFA, ffs. AVERAGE. APPROXIMATE.


Again, no, it does not. Yet again you show your utter inability to interpret data correctly. Stop deliberately and willfully citing dumb-ass values you pluck from your derrier and attribute to my data.

Quite why I am still wasting any time with you is beyond me.

Given the hand-holding you have had there is absolutely NO WAY that you don't KNOW you are talking crap.

Tell you what, I'll see if I can get David to drop by the911forum, help you out like

This is why it's better to think in terms of a confidence interval at each measurement of acceleration rather than "margin of error", which focuses the mind automatically on a possibly wrong midpoint value.

Chris7 seems to think that because "g" falls within a confidence interval of your data at each time slice, that it confirms FFA. He doesn't apparently realize that at each time slice, the actual acceleration may be anywhere within the confidence interval - generally following a gaussian (bell curve) it could be at the midpoint of the confidence interval, but since it is a probability distribution it may be anywhere within the confidence interval at any time slice. This is also why he cannot claim it is constant. It may or may not be g at every point.

Of course at root is the problem that he thinks it must be FFA because he thinks that proves his case. In reality, an acceleration of near g may (and probably did, since the penthouse collapsed first) be caused by the applied force of the interior collapse counterbalancing, and possibly overcoming, the residual resistance of the exterior columns as they failed.

 

[W.D.Clinger]

Now let's go to Mark Lindeman's post and my response at the top of this page, where he talks about an "error bar," which to my knowledge does not exist in any of NIST's, femr's or Chandler's graphs.

That's right. He made that term up. It's bombastic obfuscation verbiage.

MarkLindeman's invented term must have caught on incredibly quickly. A Google search on "error bar" already shows more than half a million hits.

MarkLindeman must have invented a time machine as well:

• According to Wikipedia's history feature, a Wikipedia article on error bar was created on 1 May 2006.
• A version of gnuplot that was installed in June 2009 and has not been modified responds to "help plot errorbars" with detailed instructions on how to use that software to plot error bars.
• The scientific literature is chock full of graphs that show error bars.

Any mistake I am making in understanding here pales in comparison to Chris7,

No, you are promoting pseudo-science from highly biased anonymous posters on a highly biased forum to refute real science.

 

[femr2]

he talks about an "error bar," which to my knowledge does not exist in any of NIST's, femr's or Chandler's graphs.

NIST do for their more refined moire analysis in Appendix C (NCStar 1-9 Vol2)...



Chandler, no.

I've suggested variance based error, such as the recent +/- 3ft/s² for acceleration (though it is possible it could be larger). Additional error discussions are buried in the "discussion of femr2's trace data" thread somewhere.

 

[MarkLindeman]

This is why it's better to think in terms of a confidence interval at each measurement of acceleration rather than "margin of error", which focuses the mind automatically on a possibly wrong midpoint value.

Yes, I agree.

MarkLindeman's invented term must have caught on incredibly quickly. A Google search on "error bar" already shows more than half a million hits.

MarkLindeman must have invented a time machine as well:

LMAO. Indeed I am peerless in the influence of my bombastic obfuscation verbiage.

Thanks. I would still be muttering to myself. How utterly, obviously, pointlessly wrong can someone be without noticing?

Kudos to femr2 for pointing out the error bars in 1-9 Appendix C.

 

[pgimeno]

as the viewpoint perspective is skewed that data is less suited to provision of derived velocity and acceleration data.

Even if so, It would be interesting to see the shape of the graph in pixels per second per second or maybe per frame per frame.

The perspective distortion should be small given the small variation in distance to the camera. It's possible to do a primitive perspective correction in the Z direction only, using the camera location and basic triangle math. The assumption that the NE corner's distance to the camera doesn't differ significantly from that of a point moving along the straight line defined by the inital NE edge of the building, is quite reasonable in my opinion.

 

[pgimeno]

Here are people who worked on 9/11 matters in one way or another. All had specialized training in whatever aspect of the work they did. Not one has come forward to support the 9/11 Truth version of events: 7,000+ FBI Agents who conducted a three-year 911 investigation; 1,500 people who worked the flight 93 crash scene; 40,000 people who worked the piles at Ground Zero; 55 FBI Evidence Response Teams at Fresh Kills in New York; 8,000+ people who worked the scene at the Pentagon. [...]

Does that mean that there were 40,000 people who didn't report evidence of devices like those proposed by Cole? Wow, that's a lot of people.

 

[pgimeno]

NIST do for their more refined moire analysis in Appendix C (NCStar 1-9 Vol2)...

[qimg]http://femr2.ucoz.com/_ph/7/2/161045534.jpg[/qimg]

I think you're assuming that C7 knows what an error bar looks like.

I think that's a wrong assumption.

Here's a little help, a search in Google Images for 'error bar':

http://images.google.com/images?q=error+bar

 

[Christopher7]

What software is that ? Draws the line ?

Asked and answered many times.
http://www.youtube.com/watch?v=rVCDpL4Ax7I

Incorrect.

My bad

And..."the AVERAGE"...finally.

Finally? I have said that many times too.

YOU don't even seem capable of correctly understanding what they are talking about, regardless of whether they do or not. Not a good starting position.

Speak for yourself.
This is perfectly clear to anyone but a denier.
"This acceleration was 32.2 ft/s2(9.81 m/s2), equivalent to the acceleration of gravity g."

They used an accepted scientific method to determine FFA.

Which was ? And ... ~FFA, ffs. AVERAGE. APPROXIMATE.

Word games. The average of the data points is FFA, well within the margin of error. Only devout deniers try to say it wasn't FFA. You are splitting hairs in a vain effort to deny what NIST and Chandler clearly stated.

FEMR's velocity graph confirms their findings of ~2.25 to 2.5s of FFA.

Again, no, it does not.

I forgot to include: "and momentary >g if you want to believe that" but I have included that several times.

Here is how I see it. Draw the line that shows your interpretation. This is not rocket science so cut the insults and be specific.

 

[femr2]

Even if so, It would be interesting to see the shape of the graph in pixels per second per second or maybe per frame per frame.

Can do.

The perspective distortion should be small given the small variation in distance to the camera. It's possible to do a primitive perspective correction in the Z direction only, using the camera location and basic triangle math. The assumption that the NE corner's distance to the camera doesn't differ significantly from that of a point moving along the straight line defined by the inital NE edge of the building, is quite reasonable in my opinion.

It's not quite that simple, as the viewpoint is off to the West of the building, and N-S motion also affects vertical trace data...as per the NIST trace which suffers from their initial data being from a point undergoing primarily N-S motion they misinterpreted as vertical.

As long as it's understood that a full 3D perspective correction has not been performed, fine.

 

[femr2]

Asked and answered many times.
http://www.youtube.com/watch?v=rVCDpL4Ax7I

Incorrect. Quote your answers to the following questions.

Use your words. A YT link does not answer your assertions about NIST and Chandler.

How did he perform the displacement data extraction ?

What program did he use ?

What mathematical method of derivation does it employ ?

How did NIST perform the displacement data extraction ?

What program did they use ?

What mathematical method of derivation did they employ ?

Finally? I have said that many times too.

Then you'll have no issue adding a ~ prefix to your "FFA" every time you state it then.

Speak for yourself.
This is perfectly clear to anyone but a denier.

ROFL. A while since I've been called a "denier". Denying what ? lol.

No-one is denying a period of ~FFA.

It's the ~ that's important there.

If you can't understant that, then there's little hope for you, and every time you omit it there will be an appropriate response, ad infinitum, ad absurdum.

"This acceleration was 32.2 ft/s2(9.81 m/s2), equivalent to the acceleration of gravity g."

Not AT. ~FFA = Fine and dandy.

The average of the data points is FFA

~FFA. How willfully and blatantly stubborn can you be ?

well within the margin of error

What is the "margin of error" ?

Only devout deniers try to say it wasn't FFA.

There's that denier moniker again. LOLz.

~FFA.

You are splitting hairs in a vain effort to deny what NIST and Chandler clearly stated.

Incorrect. I'm imposing correctness and accuracy.

What difference does the "~" make to your "argument" ?

Don't ingnore this...

What caused early motion of the building, as-in...the building was in motion long before it started to drop. What caused that motion ?

I forgot to include: "and momentary >g if you want to believe that" but I have included that several times.

Omission of the >g period is not the problem. Erroniously adding half a second to even a generous estimation of ~FFA period is the problem.

The ONLY reason you're doing that is to try and pretend that you can get the same numbers from my data that you want to match those (different) values you are obsessed with from NIST and Chandler.

Obvious. Transparent. Incorrect.

Here is how I see it.

And that's your problem.

Draw the line that shows your interpretation.

Sure...


My acceleration graph shows:

a) Rapid increase in acceleration from release to somewhat over-g in approximately 1s.

At the end of this period, the NW corner had descended ~9ft

b) Slow reduction in acceleration to approximately g over approximately 1.5s.

At the end of this period, the NW corner had descended ~83ft

c) More rapid reduction in acceleration to roughly constant velocity over approximately 2s.

At the end of this period, the NW corner had descended ~270ft

This is not rocket science

Correct.

so cut the insults

Get a grip.

and be specific.

Oh, the irony. What is it that you think I'm doing OTHER than being specific ?

 

[pgimeno]

It's not quite that simple, as the viewpoint is off to the West of the building, and N-S motion also affects vertical trace data...as per the NIST trace which suffers from their initial data being from a point undergoing primarily N-S motion they misinterpreted as vertical.

Perspective projection (and thus correction) depends on distance to the camera. Approximately constant distance (or with a negligible percent in variation, as in the case of the Dan Rather viewpoint) results in negligible need for correction.

Anyway, it's possible to add error bars to the data points corresponding to the maximum possible N-S motion, telling the maximum variation in vertical distance resulting from that motion. I expect these error bars to be very small. I can help with the calculations if necessary.

E-W movement info from the Dan Rather view would help too. Even more: in theory, these two videos should be enough to determine the 3D movement of the corner, because the intersection of two lines (in this case the "ray" going from the camera to the NW corner, from each of the videos) uniquely determines a point, unless the lines are parallel which is not the case. With that 3D info it would then be possible to perform full perspective correction.

It's a big project though. Not sure if my own motivation reaches that far. I'm busy helping Chris Mohr for now.

As long as it's understood that a full 3D perspective correction has not been performed, fine.

For now I'm interested in the shape of the curve for the first moments. There's little N-S movement at that point. I haven't compared the height of the windows near the bottom with that near the top; that can also give an idea of the influence of perspective.

 

[chrismohr]

I am now up to Reason #20 (second draft) at www.chrismohr911.com. There will also be a pass-through of logical issues, a summary of which several of u are working on now. There will also be more links. Comments and suggested links welcome.