Magnetic reconnection and physical processes

[Zeuzzz]

This thread is an attempt to try to resolve the long debate on magnetic reconnection that has been ongoing in various threads, which I now feel needs its very own thread. I have spent ages trying to get a concrete definition of magnetic reconnection from someone, everyone seems to give different answers, and there are a lot of separate things that need to be taken into account, so here’s the chance for Sol and others to write exactly what magnetic reconnection is. I am after the whole process, from the topological change in the field lines representing the magnetic vector field around the formation of the neutral point (often respresentaed as an X type neutral line) all the way through to how the energy is physically released from the topology of the lines in this system.

So it would be helpful if someone could write what they consider to be a complete and full description of the entire process of magnetic reconnection and how it relates to physical real world processes and the energy it releases.

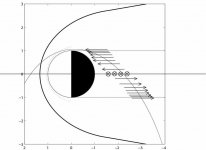
This is what I understand to be the uncontroversially accepted magnetic field configuration associated with magnetic reconnection;






"The standard explanation of reconnection (above) is that magnetic field lines 1 and 2 move in from the left and from the right, and eventually come together (short circuit) at the central point. There they change their structure: The two top halves join (reconnect) and move up, ultimately reaching the position of line 3, while the two bottom halves join and form the line that later moves to position 4. [....] In this reconnected configuration, the field lines are bent tightly like the elastic strings of a catapult. When the field lines suddenly straighten, they supposedly fling out plasma in opposite directions. " - (ref)


Other things that need to be discussed in this thread are:



A) The difference between field lines reconnecting in the formation of a standard neutral point and what physically occurs (if anything) when this happens, and what physically occurs in magnetic reconnection used to explain various energy releasing mechanisms in astrophysics.

B) The difference between field line reconnection in normal matter, ie, solid, liquid and gas, and field line reconnection in the fundamental state of matter, plasma. I suspect we need to give both different names to avoid confusion. (This is a similar question to A), and they may mean basically the same thing [depending on how you define MR])

C) The concept of moving magnetic field lines in the first place, and what this physically means in the real world.

D) The magnetohydrodynamic terms used to define magnetic reconnection, how they apply, and their validity (such as magnetic tension/pressure and the frozen field line concept)

E) The reconnection rate. This is arbitrarily set for each event in MHD simulations. Some say this is a problem, and it should have a definitive value.

F) Whether current disruption is a viable and less problematic alternative to magnetic reconnection in all situations. If not, why not, and under what circumstances.

G) Whether magnetic reconnection is an example of reifying an abstract theoretical concept (some say that field lines are not real-world 3-D entities and thus cannot do anything, like mathematical singularities, field lines are pure abstractions and cannot be reified into being real 3-D material objects)

H) Which quantity (time-varying electric current or moving magnetic “lines”) causes energy release from the plasma.

I) Whether the Ej approach has any advantages over the Bu approach, and the differences between them in explaining the phenomenon called magnetic reconnection (current disruption in the former, and magnetic reconnection in the latter). Also which is primary of the two approaches may be a good idea, as this seems to be in dispute as well, but I'm fairly sure it has been shown that they are not equivalent in all respects, despite being derived from equivalent versions of maxwells equations. Which can be somewhat confusing.

J) Whether Alfvens plasma double layer based current disruption alternative to MR is correct, which he concluded was likely from noting that the second term in the MHD equation that magnetic reconnection is based on (( ∇ (p + B² / 2μ_o ) − (B∇) B / μ₀ = 0 )) is equivalent to the pinch effect caused by electric currents. He contended that If the currents are disrupted (by an exploding double layer in their path), the field will quickly collapse and liberate all of the energy that is stored in the magnetic field that surrounds the conductors.




If anyone thinks they have answers to any of these questions, please give your two cents worth. And I'll give my opinion on each as the thread progresses. This topic has far too many ambiguous questions for simple answers. Some have ascertained that it makes no sense to ask some of these questions, and even top experts in this field find it very hard to agree on some of these issues. (See also Lui, EOS, Vol. 83, No. 41, 8 October 2002)



A very brief background on this debate for those unfamiliar. Hannes Alfven was the nobel prize winner in physics for his work on plasmas many years ago, and (amongst many other things) came up with the concept of frozen in field lines and moving magnetic field lines to explain various things in plasma physics. He later re-evaluated this idea after some serious contemplation; unfortunately he did this after the idea had become an entrenched tool in most standard astrophysics models, and he used his 1970 acceptance speech for the Nobel Prize in physics to try to warn people that this frozen-in idea was false. In reality, magnetic fields do move with respect to plasma cells and, in doing so, induce electric currents. Alfvén said, “I thought that the frozen-in concept was very good from a pedagogical point of view, and indeed it became very popular. In reality, however, it was not a good pedagogical concept but a dangerous ‘pseudo pedagogical concept.’ By ‘pseudo pedagogical’ I mean a concept which makes you believe that you understand a phenomenon whereas in reality you have drastically misunderstood it.” Such a move, effectively ruling out his own popular theory, showed great integrity as a scientist.

Due to this Alfven became a severe critic of the concept of magnetic reconnection, which was based nearly entirely on these ideas he since dismissed. He said; “Of course there can be no magnetic merging energy transfer. The most important criticism of the merging mechanism is that by Heikkila, who, with increasing strength, has demonstrated that it is wrong. In spite of all this, we have witnessed, at the same time, an enormously voluminous formalism building up based on this obviously erroneous concept.

I was naïve enough to believe that [magnetic recombination] would die by itself in the scientific community, and I concentrated my work on more pleasant problems. To my great surprise the opposite has occurred: ‘merging’ . . . seems to be increasingly powerful. Magnetospheric physics and solar wind physics today are no doubt in a chaotic state, and a major reason for this is that part of the published papers are science and part pseudoscience, perhaps even with a majority in the latter group.” However, despite his warnings, through a mixture of the gold effect and other people popularizing magnetic reconnection, it has become a vital part of many astrophysical models, with most people ignoring the underlying problems with the theory.

And thats where we are today. Some people agree with MR and use it in all of their models to explain various energetic phenomenon in space, some don't think it can happen at all like MR theory says it does, and consider alternatives like current disruption (and other variants) to be more viable and far better at explaining observations in each situation. An overview of some of the differences in opinion that have emerged can be seen in this publication from the IEEE Transactions on Plasma Science, which mostly defends Alfvens views; Real Properties of Electromagnetic Fields and Plasma in the Cosmos [D. Scott, Vol. 35, NO. 4, August 2007]

 

[tusenfem]

"The standard explanation of reconnection (above) is that magnetic field lines 1 and 2 move in from the left and from the right, and eventually come together (short circuit) at the central point. There they change their structure: The two top halves join (reconnect) and move up, ultimately reaching the position of line 3, while the two bottom halves join and form the line that later moves to position 4. [....] In this reconnected configuration, the field lines are bent tightly like the elastic strings of a catapult. When the field lines suddenly straighten, they supposedly fling out plasma in opposite directions.

Yes, that is the very simplified description of reconnection. However, you need to take into account that the "density of field lines" gives the magnetic field strength and in the "reconnection region" naturally the field strength goes to zero and the idea of a field line does not make sense anymore.

Apart from that "when the field lines suddenly straighten" that is caused by the magnetic tension, just like a pulled string.

For the rest, I have discussed reconnection in its simple form on BAUT and I don't feel like copy-pasting. Because there are several follow up posts. I guess I will have to put this into my "plasma physics for dummies" document, that I am producing for BAUT.

 

[sol invictus]

These are mostly reasonable questions, so I'll answer a few. I suggest you read the link tusenfem (who is clearly an expert on this topic, which I am not) posted.

A) The difference between field lines reconnecting in the formation of a standard neutral point and what physically occurs (if anything) when this happens, and what physically occurs in magnetic reconnection used to explain various energy releasing mechanisms in astrophysics.

I can't answer that without knowing what you mean by "standard neutral point". If you are referring to the B field configuration Zig and I posted months ago, I have a question for you: what is the current density in that configuration?

B) The difference between field line reconnection in normal matter, ie, solid, liquid and gas, and field line reconnection in the fundamental state of matter, plasma. I suspect we need to give both different names to avoid confusion. (This is a similar question to A), and they may mean basically the same thing [depending on how you define MR])

I think that what matters the most is the conductivity and fluid properties of the material. I don't see why reconnection very similar to the plasma version couldn't take place in another material with similar such properties. I would define "magnetic reconnection" itself as any process in which B lines reconnect. The amount of energy released depends strongly on the material the current flows in.

C) The concept of moving magnetic field lines in the first place, and what this physically means in the real world.

There's something very basic you have not been able to grasp about B field lines. I've attempted to explain it to you many times without success. I'll try once more: B field lines are a way of representing a magnetic field. When the field changes, the field lines change and move. One can fully characterize the field by its lines - in the limit of infinite line density, all the information about the field is contained in the line configuration. So moving field lines indicate that the field is changing. Reconnecting lines indicate the field is changing in a particular way.

It is perfectly valid to endow the lines with quantities like energy, because their density is the energy density. In fact, the fields themselves are simply convenient abstractions to keep track of electromagnetic forces - they are no more or less "real" than the lines. You would do well to try to understand this.

D) The magnetohydrodynamic terms used to define magnetic reconnection, how they apply, and their validity (such as magnetic tension/pressure and the frozen field line concept)

See tusenfem's link.

Enough for now.

 

[Gravy]

I have spent ages trying to get a concrete definition of magnetic reconnection...and how it relates to physical real world processes and the energy it releases.

I've been engaged to the same woman five times. Numerous physical processes were involved. Each time an immeasurably large amount of energy was released. Oh, and I'm about to move to the city where she lives.

 

[Zeuzzz]

There's something very basic you have not been able to grasp about B field lines. I've attempted to explain it to you many times without success. I'll try once more: B field lines are a way of representing a magnetic field. When the field changes, the field lines change and move. One can fully characterize the field by its lines - in the limit of infinite line density, all the information about the field is contained in the line configuration. So moving field lines indicate that the field is changing. Reconnecting lines indicate the field is changing in a particular way.

I would have to disagree when you say that "One can fully characterize the field by its lines - in the limit of infinite line density, all the information about the field is contained in the line configuration."

Every magnetic field is a continuum, i.e., a vector field. Each of the infinite and uncountable points in this continuum has a magnitude and a direction that is associated with it. This continuum is not made of (does not contain) a set of discrete lines. Lines can be drawn on paper to describe the magnetic fields direction and magnitude, however the field itself is not made of these lines.

Another thing, you say "So moving field lines indicate that the field is changing." Yes, that is indeed true. But I dont think that the field underlying our model of it realises this. What is changing in MR is the topology of the the lines we use to measure the field. The actual strength of the field is not inordinantly reduced in any place, it is still a continuum, even though the lines we are using to model this continuum have to change topology and 'reconnect' to remain an accurate representation of the vector field.

 

[Zeuzzz]

Yes, that is the very simplified description of reconnection. However, you need to take into account that the "density of field lines" gives the magnetic field strength and in the "reconnection region" naturally the field strength goes to zero and the idea of a field line does not make sense anymore.

hmmm, if in the reconnection region the strength goes to zero (its essentially a neutral point, correct?) how can any energy be liberated from a region where no magnetic energy is stored?

The energy stored at a point in a B-field is proportional to the square of the magnitude of the magnetic flux density at that point, so if B = 0 then the stored energy has to be W_B = 0.

ie, for the relationship: [latex]W_b=\frac{1}{2{\mu}_0}\int{{B}^2_I}dv[/latex] (where B_I is the magnitude of the magnetic field, and dv is a small volume element)

Correct me if i'm wrong here.

Apart from that "when the field lines suddenly straighten" that is caused by the magnetic tension, just like a pulled string.

This is what I find dubious. The field lines are literally assigned a tension. How can you do this? What experimental evidence do we have that the field lines themselves can possess a tension? To me it all leads to completely redefining what field lines are. Pulling something 'like a string' is a physical process. Field lines, like vectors or singularities, are not physical things, so you shouldn't be able to do anything physical like this to them.

To me this is like saying that the equator of the Earth gets pulled along and stretched slightly as cars drive over it. The equator doesn't physically exist to enable such an action. Its a line put in by us to help model aspects of the Earths climate, and other things.

To me, the motion of magnetic field lines in this sense is inherently meaningless. The magnetic field is a vector field defined as a function of space coordinates and time. At a fixed time, you can trace a field line from a given point in space. But that field line has no identity, and in a time-dependent magnetic field it cannot be identified with any field line at a different time. Magnetic field “lines” do not actually exist in three-dimensional space and therefore cannot move. They are simply graphic artifices to aid visualization of the field’s strength and direction. A magnetic field is a continuum, not a set of discrete lines.

For the rest, I have discussed reconnection in its simple form on BAUT and I don't feel like copy-pasting. Because there are several follow up posts. I guess I will have to put this into my "plasma physics for dummies" document, that I am producing for BAUT.

Thanks for that. When I've more time I'll read through this and come up with what bothers me about MR. Looks like quite a lot was discussed in that thread, its really long, maybe everythings been covered there.

Why is it locked? I always notice that happens at baut. Can be very, very annoying for people wanting to continue discussions.

Edit: Just noticed that DeiRenDopa (formerly known as Nereid) was contributing to that thread. I think I know who locked it now.

(And you have a link to DrRockets 'debate' with mike you mentioned in the last post? gotta see that one )

 

[sol invictus]

I would have to disagree when you say that "One can fully characterize the field by its lines - in the limit of infinite line density, all the information about the field is contained in the line configuration."

You can disagree all you like, but what I said is correct. Would you like me to prove it mathematically?

Another thing, you say "So moving field lines indicate that the field is changing." Yes, that is indeed true. But I dont think that the field underlying our model of it realises this.

Gibberish.

What is changing in MR is the topology of the the lines we use to measure the field.

The topology is one thing that is changing. The lines are also moving.

The actual strength of the field is not inordinantly reduced in any place, it is still a continuum, even though the lines we are using to model this continuum have to change topology and 'reconnect' to remain an accurate representation of the vector field.

Wrong. Watch the simulation I linked to for you months ago. The field strengths are changing very rapidly, because when the lines snap they get flung out towards the sides.

hmmm, if in the reconnection region the strength goes to zero (its essentially a neutral point, correct?) how can any energy be liberated from a region where no magnetic energy is stored?

Learn some basic calculus and you'll understand.

The energy stored at a point in a B-field is proportional to the square of the magnitude of the magnetic flux density at that point, so if B = 0 then the stored energy has to be W_B = 0.

The energy stored at any point is zero.

Correct me if i'm wrong here.

You're wrong. It's true that the energy density at a point is zero if the B field is zero there, but the density at a point is meaningless. Densities only mean something after you integrate them. As I explained to you many times, when lines reconnect they straighten and untangle themselves, thereby greatly reducing the energy density in the field in that region.

This is what I find dubious. The field lines are literally assigned a tension. How can you do this? What experimental evidence do we have that the field lines themselves can possess a tension? To me it all leads to completely redefining what field lines are. Pulling something 'like a string' is a physical process. Field lines, like vectors or singularities, are not physical things, so you shouldn't be able to do anything physical like this to them.

You misunderstand this at such a fundamental level I don't know where to even start. No one is assigning any new properties to anything. All we need are Maxwell's equations in plasma. Field lines and their behavior are a way to describe the solutions to those equations. Those solutions behave as we've been telling you. There is nothing more and nothing less. If you don't like field lines you can represent the solution in some other way. Be my guest... but you'll never make any progress.

To me, the motion of magnetic field lines in this sense is inherently meaningless.

Then you have understood nothing. You need to go away and think this through for yourself - at this point I don't think there is any way anyone can explain it to you. I suggest you buy Griffiths' introduction to EM and read it, especially the first few chapters.

 

[DeiRenDopa]

[...]

For the rest, I have discussed reconnection in its simple form on BAUT and I don't feel like copy-pasting. Because there are several follow up posts. I guess I will have to put this into my "plasma physics for dummies" document, that I am producing for BAUT.

Thanks for that. When I've more time I'll read through this and come up with what bothers me about MR. Looks like quite a lot was discussed in that thread, its really long, maybe everythings been covered there.

Why is it locked? I always notice that happens at baut. Can be very, very annoying for people wanting to continue discussions.

Edit: Just noticed that DeiRenDopa (formerly known as Nereid) was contributing to that thread. I think I know who locked it now.

(And you have a link to DrRockets 'debate' with mike you mentioned in the last post? gotta see that one )

Well thank you Z!

If any reader wishes to click on the link in tusenfem's post, they will find themselves in a BAUT thread ... in its "Against the Mainstream" (a.k.a. ATM) section.

Said reader will discover something very interesting ... all threads in that ATM section that are more than 30 days' old (from the date of the OP) are locked!

Yep, that's right, all threads, with no exceptions.

Clearly this is an insidious plot to viciously (or viscously, as you choose) suppress free-thinking sceptics.

Or is there a more mundane explanation?

Stay tuned for the next exciting episode of "Believe it or not, Z cannot read!".

 

[Zeuzzz]

You can disagree all you like, but what I said is correct. Would you like me to prove it mathematically?



Gibberish.



The topology is one thing that is changing. The lines are also moving.



Wrong. Watch the simulation I linked to for you months ago. The field strengths are changing very rapidly, because when the lines snap they get flung out towards the sides.



Learn some basic calculus and you'll understand.



The energy stored at any point is zero.



You're wrong. It's true that the energy density at a point is zero if the B field is zero there, but the density at a point is meaningless. Densities only mean something after you integrate them. As I explained to you many times, when lines reconnect they straighten and untangle themselves, thereby greatly reducing the energy density in the field in that region.



You misunderstand this at such a fundamental level I don't know where to even start. No one is assigning any new properties to anything. All we need are Maxwell's equations in plasma. Field lines and their behavior are a way to describe the solutions to those equations. Those solutions behave as we've been telling you. There is nothing more and nothing less. If you don't like field lines you can represent the solution in some other way. Be my guest... but you'll never make any progress.



Then you have understood nothing. You need to go away and think this through for yourself - at this point I don't think there is any way anyone can explain it to you. I suggest you buy Griffiths' introduction to EM and read it, especially the first few chapters.

As usual sol you've handpicked small sentences and made sweeping remarks without explaining yourself or considering what I was actually saying. I'll reply to each of these tomorrow when I've the time.

Meanwhile, care to comments on the two main points I made in each post, that you completely ignored? Mainly the statements:

Every magnetic field is a continuum, i.e., a vector field. Each of the infinite and uncountable points in this continuum has a magnitude and a direction that is associated with it. This continuum is not made of (does not contain) a set of discrete lines. Lines can be drawn on paper to describe the magnetic fields direction and magnitude, however the field itself is not made of these lines.

and

To me, the motion of magnetic field lines in this sense is inherently meaningless. The magnetic field is a vector field defined as a function of space coordinates and time. At a fixed time, you can trace a field line from a given point in space. But that field line has no identity, and in a time-dependent magnetic field it cannot be identified with any field line at a different time. Magnetic field “lines” do not actually exist in three-dimensional space and therefore cannot move. They are simply graphic artifices to aid visualization of the field’s strength and direction. A magnetic field is a continuum, not a set of discrete lines.

 

[Zeuzzz]

Well thank you Z!

If any reader wishes to click on the link in tusenfem's post, they will find themselves in a BAUT thread ... in its "Against the Mainstream" (a.k.a. ATM) section.

Said reader will discover something very interesting ... all threads in that ATM section that are more than 30 days' old (from the date of the OP) are locked!

Yep, that's right, all threads, with no exceptions.

Clearly this is an insidious plot to viciously (or viscously, as you choose) suppress free-thinking sceptics.

Or is there a more mundane explanation?

Stay tuned for the next exciting episode of "Believe it or not, Z cannot read!".

I didn't know that. And who was responsible for the decision that all threads in that section that are more than 30 days' old should be locked? why would anyone do that anyway?

Do you want me to compile a long list of all the threads that you have locked yourself? spare me the effort. This sort of censorship behaviour doesn't do your cause any favors, it just angers people that want to talk about stuff but get stopped from doing so. It just hardens attitudes.

 

[sol invictus]

Every magnetic field is a continuum, i.e., a vector field. Each of the infinite and uncountable points in this continuum has a magnitude and a direction that is associated with it. This continuum is not made of (does not contain) a set of discrete lines. Lines can be drawn on paper to describe the magnetic fields direction and magnitude, however the field itself is not made of these lines.

Ignored? What are you talking about? I just told you - in the limit of large line density the lines fully characterize the field - and I offered to prove it. Are you having trouble understanding English?

To me, the motion of magnetic field lines in this sense is inherently meaningless. The magnetic field is a vector field defined as a function of space coordinates and time. At a fixed time, you can trace a field line from a given point in space. But that field line has no identity, and in a time-dependent magnetic field it cannot be identified with any field line at a different time. Magnetic field “lines” do not actually exist in three-dimensional space and therefore cannot move. They are simply graphic artifices to aid visualization of the field’s strength and direction. A magnetic field is a continuum, not a set of discrete lines.

And I also responded to this.

It's not even wrong; it simply repeats the garbage you've been spewing for months and months. You have utterly failed to comprehend even the basics of this after hundreds of explanatory posts from several experts. At this point, all I can conclude is that you are simply not mentally equipped to understand it.

 

[DeiRenDopa]

Well thank you Z!

If any reader wishes to click on the link in tusenfem's post, they will find themselves in a BAUT thread ... in its "Against the Mainstream" (a.k.a. ATM) section.

Said reader will discover something very interesting ... all threads in that ATM section that are more than 30 days' old (from the date of the OP) are locked!

Yep, that's right, all threads, with no exceptions.

Clearly this is an insidious plot to viciously (or viscously, as you choose) suppress free-thinking sceptics.

Or is there a more mundane explanation?

Stay tuned for the next exciting episode of "Believe it or not, Z cannot read!".

I didn't know that. And who was responsible for the decision that all threads in that section that are more than 30 days' old should be locked? why would anyone do that anyway?

Do you want me to compile a long list of all the threads that you have locked yourself? spare me the effort. This sort of censorship behaviour doesn't do your cause any favors, it just angers people that want to talk about stuff but get stopped from doing so. It just hardens attitudes.

That didn't take long now did it?

I think any reader who wants to can find who decided to make the changes to BAUT forum policy, and why ... after all, the owner of the site himself posted the reasons in stickies!

Stay tuned for the next exciting episode of "Believe it or not, Z cannot read!"

... or perhaps no need to stay tuned, almost every one of his posts is just such an episode.

 

[Zeuzzz]

I would have to disagree when you say that "One can fully characterize the field by its lines - in the limit of infinite line density, all the information about the field is contained in the line configuration."

You can disagree all you like, but what I said is correct. Would you like me to prove it mathematically?

Yeah, go on then. Hows about addressing the other part of this sentence that you cut out above where I actually explain the reasoning for this statement?

Every magnetic field is a continuum, i.e., a vector field. Each of the infinite and uncountable points in this continuum has a magnitude and a direction that is associated with it. This continuum is not made of (does not contain) a set of discrete lines. Lines can be drawn on paper to describe the magnetic fields direction and magnitude, however the field itself is not made of these lines.

Another thing, you say "So moving field lines indicate that the field is changing." Yes, that is indeed true. But I dont think that the field underlying our model of it realises this.

Gibberish.

Not at all. The fact that you say this merely shows that you either dont comprehend what I am saying or just deny that it is a viable position to take. Magnetic field “lines” are simply graphic artifices to aid visualization of the field’s strength and direction, the magnetic field they are representing is however a continuum, not a set of discrete lines. So basing things like MR on the lines themselves, that we put in, is plain wrong.

For example, can you see the problem with this statement from NASA:

http://www-istp.gsfc.nasa.gov/Education/wfldline.html
"For many years [these lines] were viewed as merely a way to visualize magnetic fields, and electrical engineers usually preferred other ways, mathematically more convenient. Not so in space, however, where magnetic field lines are fundamental to the way free electrons and ions move. These electrically charged particles tend to become attached to the field lines on which they reside, spiralling [sic] around them while sliding along them, like beads on a wire."

Can you not see how the actual field lines themselves have become Reified in this sense? This is a classic logical fallacy, see: Reification (fallacy)

What is changing in MR is the topology of the the lines we use to measure the field.

The topology is one thing that is changing. The lines are also moving.

Magnetic field lines can not move independantly. They do one job, and one job only: describe the field strength of the vector field they are modelling. Nothing more, nothing less.

The actual strength of the field is not inordinantly reduced in any place, it is still a continuum, even though the lines we are using to model this continuum have to change topology and 'reconnect' to remain an accurate representation of the vector field.

Wrong. Watch the simulation I linked to for you months ago. The field strengths are changing very rapidly, because when the lines snap they get flung out towards the sides.

The field strengths are changing, but not in any dramatic way like the field lines that are modelling the field imply. Although the proposed reconnection mechanism changes the topology of the magnetic field, it does not explicitly reduce the strength of any part of the magnetic field beyond the normal change.

hmmm, if in the reconnection region the strength goes to zero (its essentially a neutral point, correct?) how can any energy be liberated from a region where no magnetic energy is stored?

Learn some basic calculus and you'll understand.

Well thanks for that brilliant explanation. Hopefully tusenfem will give a slightly more productive answer. Thas why I asked him, not you.

The energy stored at a point in a B-field is proportional to the square of the magnitude of the magnetic flux density at that point, so if B = 0 then the stored energy has to be WB = 0.

The energy stored at any point is zero.

Your just being pedantic here. Lets change that to the energy stored around any point then, and you certainly cant say that. What I mean is that at the reconnection region it is a neutral point (or line), and the field strength is zero. At all other points (regions) of the field the strength is non zero.

Correct me if i'm wrong here.

You're wrong. It's true that the energy density at a point is zero if the B field is zero there, but the density at a point is meaningless. Densities only mean something after you integrate them. As I explained to you many times, when lines reconnect they straighten and untangle themselves, thereby greatly reducing the energy density in the field in that region.

No, i'm afraid that i'm right. I agree with this: "It's true that the energy density at a point is zero if the B field is zero there, but the density at a point is meaningless. Densities only mean something after you integrate them." I disagree with this: "when lines reconnect they straighten and untangle themselves, thereby greatly reducing the energy density in the field in that region."

I fail to see how lines representing nothing more than equal values of vectors in a vector field can become tangled. Something being tangled implies physical processes. They are not tangled, they can not fling anything out, they are just doing what they always do, representing the continuum of the infinite vector field.

This is what I find dubious. The field lines are literally assigned a tension. How can you do this? What experimental evidence do we have that the field lines themselves can possess a tension? To me it all leads to completely redefining what field lines are. Pulling something 'like a string' is a physical process. Field lines, like vectors or singularities, are not physical things, so you shouldn't be able to do anything physical like this to them.

You misunderstand this at such a fundamental level I don't know where to even start. No one is assigning any new properties to anything. All we need are Maxwell's equations in plasma. Field lines and their behavior are a way to describe the solutions to those equations. Those solutions behave as we've been telling you. There is nothing more and nothing less. If you don't like field lines you can represent the solution in some other way. Be my guest... but you'll never make any progress.

There are other ways. Without the need to consider field lines at all you can consider the currents instead, the Ej approach. By focussing on electric field and current as primary quantities you can consider an analysis based on particle dynamics, instead of the interaction of ambiguos field lines, that lead to many problems. The E-j paradigm can be considered as the approach of single particle calculation or kinetic analysis, and is useful to treat many macroscopic magnetospheric problems that cannot be explained with the B-u approach.

My main objection to the B-u paradigm is its reliance on magnetohydrodynamics, when many of the processes occurring in the magnetic reconnection are inherently kinetic, requiring an approach that can better be summed up by the E-j paradigm. There is no doubt that magnetic reconnection is useful in terms of finding the total magnetic flux injected into a system, but the question is if this is really a full and complete description of what is occuring. I dont think it is. And I think that current disruption offers a more complete kinetic description of what is physically occuring.

To me, the motion of magnetic field lines in this sense is inherently meaningless.

Then you have understood nothing. You need to go away and think this through for yourself - at this point I don't think there is any way anyone can explain it to you. I suggest you buy Griffiths' introduction to EM and read it, especially the first few chapters.

And I suggest you buy the slightly more up to date Eos, Transactions, American Geophysical Union, Vol. 88, 2007, where respected astronomer Carl-Gunne Fälthammar says the exact same thing about the idea of moving magnetic field lines that I just stated in the above quote. To quote him:

http://sprg.ssl.berkeley.edu/adminstuff/webpubs/2007_eos_169

The basic reason for these difficulties with ‘moving’ magnetic field lines is, of course, that motion of magnetic field lines is inherently meaningless. The magnetic field B is a vector field defined as a function of space coordinates and time. At a fixed time, one may trace a field line from any given point in space. But that field line has no identity, and in a time-dependent magnetic field it cannot be identified with any field line at a different time, except by one convention or another.
As we have seen, such conventions are fraught with pitfalls and should only be used with utmost care lest they lead to erroneous conclusions. To paraphrase Ralph Nader, moving magnetic field lines are “unsafe at any speed.”

 

[tusenfem]

hmmm, if in the reconnection region the strength goes to zero (its essentially a neutral point, correct?) how can any energy be liberated from a region where no magnetic energy is stored?

The energy stored at a point in a B-field is proportional to the square of the magnitude of the magnetic flux density at that point, so if B = 0 then the stored energy has to be W_B = 0.

ie, for the relationship: [latex]W_b=\frac{1}{2{\mu}_0}\int{{B}^2_I}dv[/latex] (where B_I is the magnitude of the magnetic field, and dv is a small volume element)

Correct me if i'm wrong here.

Well, your quation is okay, however, you fail to understand that it is a volume integral and to get a meaning full result you need to take a meaningful volume.

Because "the magnetic field is a continuum", better said the magnetic field is an additive vector field, i.e. two separate fields add vectorially, ther must be a region where B -> 0 if, like in the Earth's magnetotail, you have field pointed towards the Earth in the north and field pointed away from the Earth in the south. Where B=0 is called the neutral sheet, and is where the cross tail current flows (perpendicular to the magnetic field).

This is what I find dubious. The field lines are literally assigned a tension. How can you do this? What experimental evidence do we have that the field lines themselves can possess a tension? To me it all leads to completely redefining what field lines are. Pulling something 'like a string' is a physical process. Field lines, like vectors or singularities, are not physical things, so you shouldn't be able to do anything physical like this to them.

If you would just take time to read a bit of basic electrodynamics than you would find that a magnetic field can be characterized by a magnetic pressure, it rolls out of the math from a fluid description of the plasma (or MHD, you know, from your hero Alfvén) and takes the value B²/2μ₀. Similarly, you can find through the Maxwell stress tensor and you find that the tension is given by (interestingly) B²/μ₀.

Now, it is pretty clear that if the magnetic field can have a tension, then logically we can attribute this tension to magnetic field lines.

And yes, we have observations of this stuff, namely when something hits the Earth's magnetosphere, then the magnetic field is compressed (increased B so increased pressure and tension) or if something disturbs a field line, setting it to oscillate, that is pure tension!! Field line resonances in the Earth's magnetosphere, which have been measured for dozens of years exist by the grace that the magnetic field has tension.

To me this is like saying that the equator of the Earth gets pulled along and stretched slightly as cars drive over it. The equator doesn't physically exist to enable such an action. Its a line put in by us to help model aspects of the Earths climate, and other things.

BUT IT DOES, the friction between the tires and the Earth is what makes your are move, apparently you don't have much knowledge of basic physics.

To me, the motion of magnetic field lines in this sense is inherently meaningless. The magnetic field is a vector field defined as a function of space coordinates and time. At a fixed time, you can trace a field line from a given point in space. But that field line has no identity, and in a time-dependent magnetic field it cannot be identified with any field line at a different time. Magnetic field “lines” do not actually exist in three-dimensional space and therefore cannot move. They are simply graphic artifices to aid visualization of the field’s strength and direction. A magnetic field is a continuum, not a set of discrete lines.

Meaningless for you, maybe, but not for Alfvén, and not for me, but then again you ain't no plasma(astro)physicist. And if you would go through the math you would find that field lines DO have identity, I only need to remind you of the frozen in field (which you don't believe, but anywhooooooo) which clearly shows that there can be identification.

You can make infinitesimally little steps in the change of the magnetic field, calculate your field lines time and again, and when you finally get your movie you will see them move, now, for good use in physics, the field lines move, whether or not between every infinitesimal step the field line disappears and is replaced by a new one is totally philosophically and reminds me of a twilight zone episode, where people get stuck between "moments" and see how blue-dressed men are building up the next "moment".

Thanks for that. When I've more time I'll read through this and come up with what bothers me about MR. Looks like quite a lot was discussed in that thread, its really long, maybe everythings been covered there.

Why is it locked? I always notice that happens at baut. Can be very, very annoying for people wanting to continue discussions.

It was locked because for ATM there is a 30 day limit on discussion.

However, there is a "general science" thread plasma physics for dummies but there is no ATM in general science.

 

[Beausoleil]

If I may...

Firstly, thanks to participants for this thread - magnetic reconnection in a "planetary" environment is something I've long wanted to understand better but never got round to studying.

Secondly, I think that there is a general conceptual problem for people with magnetic field lines. So those of you who deal with this all the time are doing a good job of explaining it to the rest of us. Sure I could read a text book, but a conversation is easier to understand and I have a mountain of text books on my desk I could read. So, again, thanks.

On reflection, I think the problem people have with lines comes down to a step something like this. You can fully characterise the field in terms of lines. Properties of the field like pressure and density can be assigned to the lines. Nonetheless, it is not the case that the field is made up of distinct lines - if you pass through a region of space you might be crossing field lines, but you don't come across them discretely. It's not "line - line free region - line - line free region..."

Is that right?

Anyway, if you could be bothered to post the link to the animation you mentioned again I'd be grateful.

 

[Zeuzzz]

Anyway, if you could be bothered to post the link to the animation you mentioned again I'd be grateful.

Thats pretty much it. Then the reified lines are presumed to fling out plasma when they connect in the centre, based on elaborate MHD models and various other attributes discussed above. The reconnection rate is always arbitrarily set in simulations. Make of it what you will.

 

[tusenfem]

On reflection, I think the problem people have with lines comes down to a step something like this. You can fully characterise the field in terms of lines. Properties of the field like pressure and density can be assigned to the lines. Nonetheless, it is not the case that the field is made up of distinct lines - if you pass through a region of space you might be crossing field lines, but you don't come across them discretely. It's not "line - line free region - line - line free region..."

Hey Beau!

Magnetic fields (an not those alone, one can do this with respect to all vector fields) have a direction and an amplitude in space and therefore we call it a vector field B(r). Now, if we know the direction in every point, then we can "connect the dots" going in tiny steps δr from point r₁ to point r₂, where the direction of this step is given by the direction of the magnetic field B at point 1. This can be integrated, and then one get, e.g. for a magnetic dipole that the field line is given by R/cos²(θ) = cst, where θ is the angle between point R and the direction of the dipole d. Note, however, that the field line by itself does NOT say anything about the strength of the magnetic field.

The strength of the magnetic field is given by the field line density, which is an abstract number that can be given to the magnetic field strength, basically you can normalize it to the magnetic flux ∫B•dS, the integral over a surface, summing the magnetic field component perpendicular to that surface. This means that when we draw field lines (or at least we should do that, but usually it is taken for a given and we forget about it in the drawing) we should draw more lines per cm when the field is stronger. I have given an example in the attachment from my latest research topic, the mangetotail of Venus. See how the arrows are closer spaced away from the center, indicating a stronger field.

However, it is always a continuous vector field, and like you say, no, there are no "steps." But the concept of field lines makes scientific life so much easier, even though it might nerve Zeuzzz out of his undies, but then, he is no scientist.

Hope this helps.

 

[Zeuzzz]

Magnetic fields (an not those alone, one can do this with respect to all vector fields) have a direction and an amplitude in space and therefore we call it a vector field B(r). Now, if we know the direction in every point, then we can "connect the dots" going in tiny steps δr from point r₁ to point r₂, where the direction of this step is given by the direction of the magnetic field B at point 1. This can be integrated, and then one get, e.g. for a magnetic dipole that the field line is given by R/cos²(θ) = cst, where θ is the angle between point R and the direction of the dipole d. Note, however, that the field line by itself does NOT say anything about the strength of the magnetic field.

The strength of the magnetic field is given by the field line density, which is an abstract number that can be given to the magnetic field strength, basically you can normalize it to the magnetic flux ∫B•dS, the integral over a surface, summing the magnetic field component perpendicular to that surface. This means that when we draw field lines (or at least we should do that, but usually it is taken for a given and we forget about it in the drawing) we should draw more lines per cm when the field is stronger. I have given an example in the attachment from my latest research topic, the mangetotail of Venus. See how the arrows are closer spaced away from the center, indicating a stronger field. View attachment 11716

However, it is always a continuous vector field, and like you say, no, there are no "steps." But the concept of field lines makes scientific life so much easier, even though it might nerve Zeuzzz out of his undies, but then, he is no scientist.

Hope this helps.

you were quite civil to begin with, but now your starting to join the jref crowd your last few posts are starting to come over all insulting. Sol and DRD's confrontational attitude seems to have this effect on other people. Sigh. Note I wont make similar remarks in return.

Either that, or instead of relying on the concept of magnetic reconnection it may be worthwhile to consider that the solar wind– magnetosphere dynamo generates two solenoidal currents in the magnetotail. I'll post this in the other thread, since you asked in that one for my alternative explanation: http://www.internationalskeptics.com/forums/showthread.php?t=121504

 

[Beausoleil]

[qimg]http://www.nature.com/nphys/journal/vaop/nprelaunch/images/nphys111-f1.gif[/qimg]


Thats pretty much it. Then the reified lines are presumed to fling out plasma when they connect in the centre, based on elaborate MHD models and various other attributes discussed above. The reconnection rate is always arbitrarily set in simulations. Make of it what you will.

Thanks.

I think the point is this. Everything about the field is described by the lines. However, whenever you draw field lines you give them a specific position which does not represent a feature of the field - the lines you draw on a figure have properties beyond those that ensure that a treatment dealing with field lines completely describes the field.

That the field lines change configuration implies that the field changes. The changing field affects plasma. I think this is reasonable, isn't it?

 

[Beausoleil]

Hey Beau!

Magnetic fields (an not those alone, one can do this with respect to all vector fields) have a direction and an amplitude in space and therefore we call it a vector field B(r). Now, if we know the direction in every point, then we can "connect the dots" going in tiny steps δr from point r₁ to point r₂, where the direction of this step is given by the direction of the magnetic field B at point 1. This can be integrated, and then one get, e.g. for a magnetic dipole that the field line is given by R/cos²(θ) = cst, where θ is the angle between point R and the direction of the dipole d. Note, however, that the field line by itself does NOT say anything about the strength of the magnetic field.

The strength of the magnetic field is given by the field line density, which is an abstract number that can be given to the magnetic field strength, basically you can normalize it to the magnetic flux ∫B•dS, the integral over a surface, summing the magnetic field component perpendicular to that surface. This means that when we draw field lines (or at least we should do that, but usually it is taken for a given and we forget about it in the drawing) we should draw more lines per cm when the field is stronger. I have given an example in the attachment from my latest research topic, the mangetotail of Venus. See how the arrows are closer spaced away from the center, indicating a stronger field. View attachment 11716

However, it is always a continuous vector field, and like you say, no, there are no "steps." But the concept of field lines makes scientific life so much easier, even though it might nerve Zeuzzz out of his undies, but then, he is no scientist.

Hope this helps.

Yes, thanks. Planetary magnetism is the (an) other end of the planetary science spectrum from my field (isotope cosmochemistry), but I've been on enough panels dealing with magnetic reconnection to want to understand it better. (Most funding panels combine experts from various fields who don't necessarily all understand one another's area.)

Are you working on Venus Express?