Where does her initial velocity of 0 come from for boith objects? If one of them is not moving, there isn't a collision (and 0 is correct) but one being 0 and the other moving does not give a 0 answer. And of course, the tower as a whole certainly moved to a very small extent in the direction the plain was moving (but definitly less than a replacement of actual mass for the m she speaks of would indicate as much of the momentum went into individual collisions of rather small particles as the plane shredded/powderes as did parts of the building. She seems a very stupid or very physics illiterate person (I'm making an assumption on that last word.)
Judy Wood's "Math"
- Thread starter Anti-sophist
- Start date
TruthSeeker1234
Banned
- Joined
- Sep 9, 2006
- Messages
- 1,756
I agree Dr. Wood doesn't always express her ideas clearly. But here is what she is getting at with the billiard ball example, I think.
Consider two balls of equal mass. Ball A is moving and ball B is at rest. A hits B. In a perfect collision, A gives all its energy to B. B begins moving at the same velocity that A was moving, but A stops moving.
This should hold true in a vertical fall. Floor A falls and hits floor B. B begins moving at the speed A was moving prior to the impact, but A must stop, and begin falling all over again. Some part of the falling mass must stop at each impact.
The situation in real life is more complicated of course. We don't have equal masses. We don't have perfect collisions. But the point she makes applies. If momentum is transferred from one object to the other, we must not forget to subtract that momentum from the first object.
Consider two balls of equal mass. Ball A is moving and ball B is at rest. A hits B. In a perfect collision, A gives all its energy to B. B begins moving at the same velocity that A was moving, but A stops moving.
This should hold true in a vertical fall. Floor A falls and hits floor B. B begins moving at the speed A was moving prior to the impact, but A must stop, and begin falling all over again. Some part of the falling mass must stop at each impact.
The situation in real life is more complicated of course. We don't have equal masses. We don't have perfect collisions. But the point she makes applies. If momentum is transferred from one object to the other, we must not forget to subtract that momentum from the first object.
No, that's not what she's getting at. She's simply, completely, utterly, stupidly wrong.
The situation in real life is that masses A and B remain in contact after collision. The total momentum afterwards is the same as before.
Mass A does not stop, but only slows down. Mass B is accelerated -- in a very short period of time -- to the same speed as Mass A now has.
NO part of the falling mass must stop at each impact. It simply is not true. To take that argument, if I go shoot at bowling pins with my .22 rifle, when I hit the pins, the pin would topple over, and the bullet would screech to a halt and drop right there on the ground in front of the pin.
Madness!
Nobody has forgotten. Once again, go take a look at Greening's paper. He doesn't forget.
TruthSeeker1234
Banned
- Joined
- Sep 9, 2006
- Messages
- 1,756
Greening:
How can we take this seriously when it so obviously disagrees with observed reality?
Wood, on the other hand, assumes material is getting pulverized into powder. This matches reality.
How do I size the picture smaller?
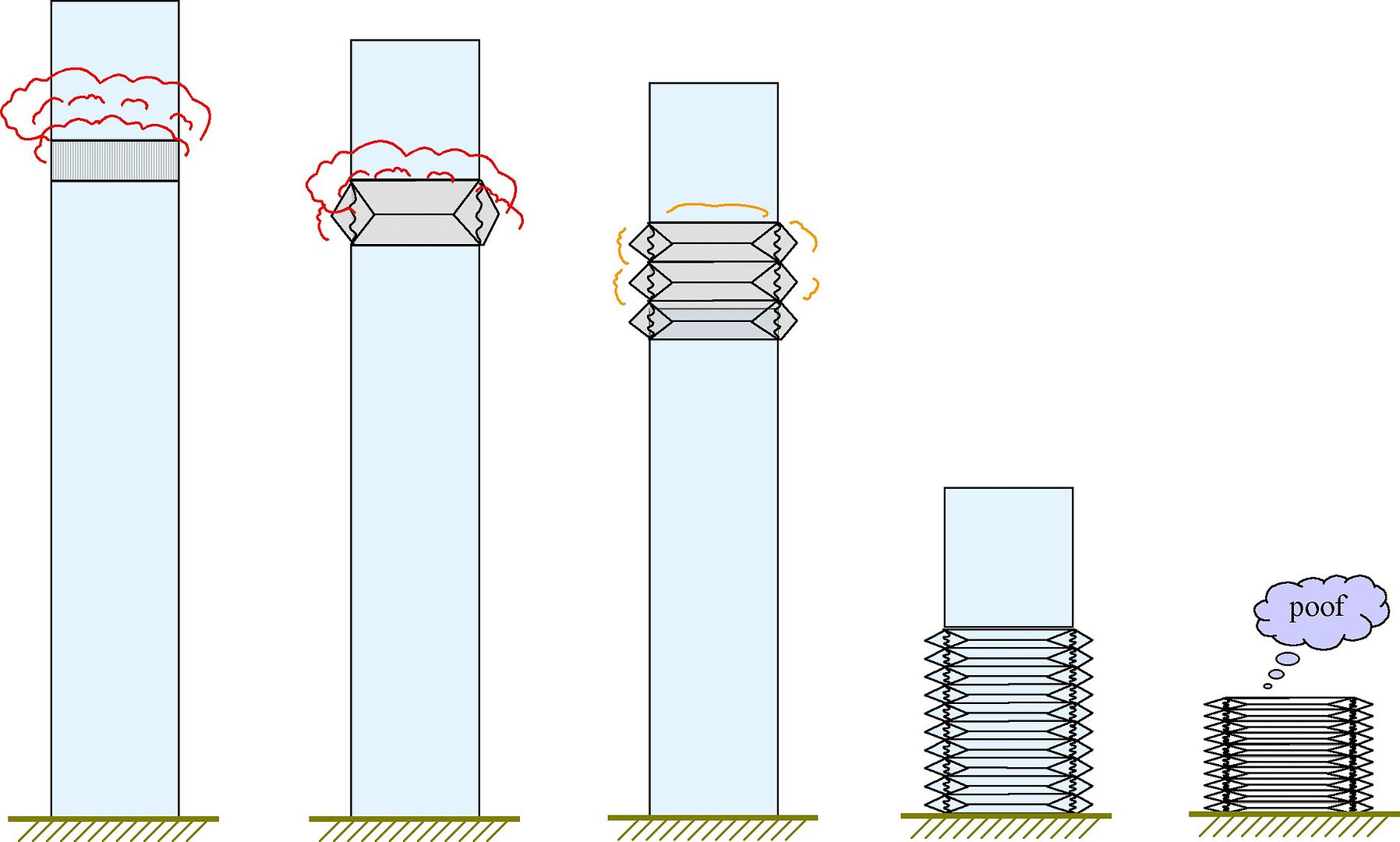
Thus, Greening, and JREF's, imagine this:
How can we take this seriously when it so obviously disagrees with observed reality?
Wood, on the other hand, assumes material is getting pulverized into powder. This matches reality.
How do I size the picture smaller?
Garb
Graduate Poster
- Joined
- Oct 15, 2006
- Messages
- 1,005
Worst. Diagram. Ever.
Anti-sophist
Graduate Poster
- Joined
- Sep 15, 2006
- Messages
- 1,542
I still can not get over the utter stupidity of the very first comment in that math.
She, literally says, "Newton's first law shows that pulverization is impossible." That is a literal math-> english translation of her argument. No explaination. Not analysis... just... that stupid statement, in mathematical form.
I can't figure out what she even is getting at. It's like a little stupid seed in my head slowly sprouting and growing stupid flowers.
She, literally says, "Newton's first law shows that pulverization is impossible." That is a literal math-> english translation of her argument. No explaination. Not analysis... just... that stupid statement, in mathematical form.
I can't figure out what she even is getting at. It's like a little stupid seed in my head slowly sprouting and growing stupid flowers.
That's indeed the same as saying that your Maxwell equations imply that I can not destroy my radio... The only thing I agree with is that the pulverization starts at an early stage, if you put your coordinate origin very high the massive pulverization starts after the initial crash already, how does it effect the momentum, maybe I'm wrong and it doesn't matter, but it should at least be a factor to take into account
Last edited:
you fell for a real nut case, Judy Wood, and you are now thinking she has something.
This is in the vertical, and these are not balls. She messed up her momentum and model of the WTC. She is proved wrong by what happen on 9/11. Until you show up with some evidence her model is junk, as are her calculation and lack of calculations.
Gravity is ignored by woods except for her cute, stop and go version of balls.
Are you Judy?
Cause the only person who could think her balls have any merit is her!
You like her beam weapon too.
You need to get an education. (did your parents us the term "pull it"? as they took away your college funds.)
delphi_ote
Philosopher
- Joined
- Jan 18, 2005
- Messages
- 5,994
Now this I have to see. TruthSeeker "interpreting" Wood. Botched physics viewed through the looking glass twice.
Gravy
Downsitting Citizen
- Joined
- Mar 27, 2006
- Messages
- 17,078
The point she makes – her whole point – is that the tower collapses should have taken over a minute and a half and could not have happened as observed due to gravity.
Now she posits that gravity's job may have been aided by a Star Wars energy beam.
Why are you CTs so afraid to say "this person is batcrap crazy, this analysis has always been laughably, horribly wrong, and we need to point that out because it's making our "movement" look ridiculous?"
twinstead
Penultimate Amazing
- Joined
- Apr 8, 2005
- Messages
- 12,374
Jesus, Gravy, if they did that in every instance they would be forced to admit that every member of their movement makes them look ridiculous.
Have you tried the above billiard ball experiment on a vertical billiard table? I know that sounds silly, but I think you might just discover something if you try it...
May I suggest you name whatever peculiar force you discover 'gravity'. I dunno why, but it just has a sort of ring to it...
delphi_ote
Philosopher
- Joined
- Jan 18, 2005
- Messages
- 5,994
Anti-sophist
Graduate Poster
- Joined
- Sep 15, 2006
- Messages
- 1,542
That's not really fair. Truthseeker's explaination is actually technically correct (that is to say, the explaination of the model is correct... the correctness of the model, on the other hand..)
If we think of a tube of equally space billard balls, vertically, and we assume that every ball is at rest by some magical force until it is contacted. Then when we drop a ball down the tube, it will hit the first ball, transfer all of it's momentum, momentarily come to rest, and then begin free-falling.
The net effect is every ball will follow the same path. It will get hit from above, inheret that speed, accelerate downwards, hit the ball below, come to a complete stop, and then enter freefall.
The net effect of this is that the "collapse wave" will proceed at freefall speed. The first ball will accelerate one floor, and transfer that velocity to the next ball who will fall at freefall acceleration, etc, etc. The "collapse wave", then, proceeds at freefall.
It's well established that the collapse doesn't proceed at freefall, so why is our model making an incorrect prediction? As has been pointed out, repeatedly, the collapse isn't elastic. An elastic model is fundamentally flawed. As has been repeatedly shown, a perfectly inelastic model of collapse is far more accurate and produces much better predictions.
I'm actually thankful for truthseeker for explaining this billiard ball model to me. The concept actually makes enough sense to be wrong. That is one step above Judy's "Newton's First Law implies pulverization is impossible". This statement makes so little sense that it brings to mind Everyones Favorite Wolfgang Pauli Quote (EFWPQ, if you will).
If we think of a tube of equally space billard balls, vertically, and we assume that every ball is at rest by some magical force until it is contacted. Then when we drop a ball down the tube, it will hit the first ball, transfer all of it's momentum, momentarily come to rest, and then begin free-falling.
The net effect is every ball will follow the same path. It will get hit from above, inheret that speed, accelerate downwards, hit the ball below, come to a complete stop, and then enter freefall.
The net effect of this is that the "collapse wave" will proceed at freefall speed. The first ball will accelerate one floor, and transfer that velocity to the next ball who will fall at freefall acceleration, etc, etc. The "collapse wave", then, proceeds at freefall.
It's well established that the collapse doesn't proceed at freefall, so why is our model making an incorrect prediction? As has been pointed out, repeatedly, the collapse isn't elastic. An elastic model is fundamentally flawed. As has been repeatedly shown, a perfectly inelastic model of collapse is far more accurate and produces much better predictions.
I'm actually thankful for truthseeker for explaining this billiard ball model to me. The concept actually makes enough sense to be wrong. That is one step above Judy's "Newton's First Law implies pulverization is impossible". This statement makes so little sense that it brings to mind Everyones Favorite Wolfgang Pauli Quote (EFWPQ, if you will).
Last edited:
Spins
Muse
- Joined
- Aug 31, 2006
- Messages
- 702
Can you imagine if Sir Isaac Newton got hit on the top of the head by a billiard ball instead of an apple!
With the brain injury he would have no doubt sustained he would have never discovered universal gravitation and the three laws of motion!
Instead of the event being called "Newton's Apple" it would have been called "Newton's Billiard Ball".
Mojo
Mostly harmless
This is a bit like like the fallacy involving an eastbound freight train hitting a westbound fly, where because the fly was originally going West but ends up going East it must at some point have been stationary, and as this must have happened when the fly was in contact with the freight train, the fly must have stopped the train!
Horatius
NWO Kitty Wrangler
- Joined
- May 9, 2006
- Messages
- 29,691
Greening:
So, out of curiosity, do you know what a physicist means when he refers to a "simple model"? Hint: They don't expect it to correspond to reality 100%.
ktesibios
Worthless Aging Hippie
- Joined
- Feb 23, 2002
- Messages
- 1,493
The thing is, even if we accept the notion that an elastic collision a' la pool balls or one of those doodads with the five steel dingleberries suspended from a frame (another example Woods uses) is an adequate analogy, her contention that the falling mass (the cue ball) should stop upon hitting the floor below (the object ball) still doesn't work.
If m1 is the mass of the "cue ball", m2 is the mass of the "object ball" and v1 and v2 are their respective velocities before the collision and v'1 and v'2 are their velocities after the collision, then the velocity of the "cue ball" after the collision is given by:
v'1=(v1(m1-m2)+2m2v2)/(m1+m2)
Okay, so if v'1 is 0, then (v1(m1-m2)+2m2v2) must be equal to 0. If v2 is 0 (the "object ball" isn't moving before the "cue ball" hits it), then 2m2v2=0, so v1(m1-m2) must equal 0. If v1 is not equal to 0 (the "cue ball" is moving before it hits the "object ball", then the only way that v'1 will come out to 0 is if m1-m2=0.
This is the case for a pool game or one of the doodads with the five steel dingleberries, but in the case of the WTC towers, m1 (the mass of the falling upper block) is obviously considerably greater than m2 (the mass of the floor it lands on).
Taking that first equation, setting v'1 to 0 and solving for v2, I get:
v2=-(v1(m1-m2))/2m2
If m1>m2 then v2 is nonzero and negative, i.e. the "object ball" must be moving towards the "cue ball" before the collision.
Even if the WTC had been built out of pool balls, for what Woods claims should have happened to happen, each floor would have had to leap upwards just before the falling mass hit it.
How you do that? Anti-gravity beams?
If m1 is the mass of the "cue ball", m2 is the mass of the "object ball" and v1 and v2 are their respective velocities before the collision and v'1 and v'2 are their velocities after the collision, then the velocity of the "cue ball" after the collision is given by:
v'1=(v1(m1-m2)+2m2v2)/(m1+m2)
Okay, so if v'1 is 0, then (v1(m1-m2)+2m2v2) must be equal to 0. If v2 is 0 (the "object ball" isn't moving before the "cue ball" hits it), then 2m2v2=0, so v1(m1-m2) must equal 0. If v1 is not equal to 0 (the "cue ball" is moving before it hits the "object ball", then the only way that v'1 will come out to 0 is if m1-m2=0.
This is the case for a pool game or one of the doodads with the five steel dingleberries, but in the case of the WTC towers, m1 (the mass of the falling upper block) is obviously considerably greater than m2 (the mass of the floor it lands on).
Taking that first equation, setting v'1 to 0 and solving for v2, I get:
v2=-(v1(m1-m2))/2m2
If m1>m2 then v2 is nonzero and negative, i.e. the "object ball" must be moving towards the "cue ball" before the collision.
Even if the WTC had been built out of pool balls, for what Woods claims should have happened to happen, each floor would have had to leap upwards just before the falling mass hit it.
How you do that? Anti-gravity beams?