Engineering help requested: Calculating stiffness of a beam

Oystein said:
Y=L^3/48 E*I is the formula for a beam simply supported on both ends for a point force in the middle. That is not the same force as the one acting on the free end, in fact it is half that force!

Now let's see if I can normalize that to the force on the free end...

To get Fend on the free end, I need to impose a lateral load in the middle of Fmiddle = 2Fend, and that gives me a deflection of

D = Fmiddle/Kmiddle = 2Fend/Kmiddle
<=> Kmiddle = 2Fend/D = 48EI/L^3
<=>Fend/D = 24EI/L^3 = Kend

Agreed? That would be 28.6 kip/in
Click to expand...
You wanted stiffness. That equation gives it to you.
 
Drewbot said:
According to this chart, it looks like steel is strongest at 440 Deg. F.

http://www.engineeringtoolbox.com/metal-temperature-strength-d_1353.html
Click to expand...

Thanks.
Is "strength" = "stiffness"? They are related - but same?
Anyway, I'll google values once I find that I need to refine my values. First I need to figure out how to get a handle on the stiffness given the geometry of my case. Then look up if and what temperature range has been determined for the girder in this fire. Then look up elastic modulus of A36 steel at that temperature.
 
Some brainstorming with pictures:

A) Treating the falling girder as a simply supported load with point load in the middle:



The stiffness formula for this situation is
Kmiddle = 48*E*I/L^3

I need to have a force F on the right end, the same F that loads the girder below.
A central force loads the end 50%:50%, so I need to apply 2F to the middle of that beam to get F at either end.

As calulated previously, this works out to a stiffness relative to an load on a free end
Kend = 24*E*I/L^3


B) Considering Angular Impulse

However, this would be justified for a beam that falls and impacts in translational motion. In that case, both ends would be equally loaded and experience an equal acceleration. This is not the case: The beam rotates, and the impact makes the free end accelerate the most, while the hinge doesn't accelerate at all (assuming it, and the column it is attached to, are infinitely stiff). The beam is continuously loaded (as if by gravity - acceleration is equivalent to gravity) along its length - not uniformly but proportional to distance from hinge:



This would also be equivalent by loading the beam with a wedge (thick end on the free end, point on the hinge). The centroid of that wedge is 2/3 L away from the hinge and 1/3 L from the free, impacting end.


C) Point load at 2/3:1/3 L

This in turn is equivalent (?) to a point load 1/3 L from the free end:



By the usual laws of levers, a load of 3/2 is distributed 1/2 : 1 to the ends.

The stiffness formula for such an off-center loaded beam is
K2/3 = 3*E*I*L / (a2 * (L-a)2)
where a = 1/3 L, so
K2/3 = 3*E*I*L / ((1/3 L)2 * (2/3 L)2) = 3*E*I*L / (4/81 L4) = 243/4 E*I / L^3

This looks weird - I am not too confident my derivation is error-free :o
 
Last edited:
I'll continue anyway:

The deflection caused by the 1.5 F load at the 2/3 point
D2/3 = F2/3 / K2/3
must be the same as a deflection caused by a loaf F at the end:
Dend = D2/3 = Fend / Kend
<=> Kend = Fend / D2/3
<=> Kend = Fend / (F2/3 / K2/3) = Fend / (3/2 Fend / K2/3) = 2/3 K2/3

<=> Kend = 2/3 * 243/4 E*I / L^3 = 81/2 E*I / L^3


Which, in my case, with
E = 29,000 kip/in^2
I = 6710 in^4
L = 547 in
is
Kend = 48.15 kip/in

Yay, I am happy :D

Unless I am wrong... :blush:
 
Looks like the right order of magnitude. It strikes me as on the soft side, I would've expected 3-4 times that or more, albeit that could be a feature of the design.
 
little soft. It is actually (Given his E, I, and L) 66.99 kip/in
Using Roark, with load at 1/3 L
Can't figure out how to past a MathCad picture in, so I'll let you look it up yourself...
 
Oystein said:
What I want to learn:

How do I determine the stiffness of the falling girder?

It is attached at its left end to a hinge about which it rotates freely, and is loaded with F perpendicular to its long axis.

...Help...?
Click to expand...

Isn't the stiffness the same whether it is falling or not? Why do you need to know and in any case the only thing of importance in this case is the strength of the end connection of the lower girder that it hits; which is presumably the same as the one that failed above.

You wouldn't be playing around with collapsing buildings when upper floors fail, like through heat weakness, would you?
 
Elind said:
Isn't the stiffness the same whether it is falling or not? Why do you need to know and in any case the only thing of importance in this case is the strength of the end connection of the lower girder that it hits; which is presumably the same as the one that failed above.

You wouldn't be playing around with collapsing buildings when upper floors fail, like through heat weakness, would you?
Click to expand...
Stiffness is a function of end conditions. A falling beam is free-free, and will be "wimpier" than one supported at the ends. A beam sitting on another beam and leaning against something is considered simply supported.at.the contact points.
However, I fail to see where the hell thus is going...
 
rwguinn said:
Stiffness is a function of end conditions. A falling beam is free-free, and will be "wimpier" than one supported at the ends. A beam sitting on another beam and leaning against something is considered simply supported.at.the contact points.
However, I fail to see where the hell thus is going...
Click to expand...

Sorry about the joke, but I still don't see why the free fall beam stiffness matters to anything, unless you are interested in the breaking force at the remaining fixed end. Stiffness can be calculated with one end fixed or both as I recall (defining displacement at a point) but if it is essentially in free fall as your example where it is simply pivoted at the "fixed" end, then what does stiffness affect?
 
OK, I'll reveal context and relevance of my question. It arose in connection with 9/11 conspiracy theories: 9/11 CTers like to focus on the collapse of the WTC building 7 (47 stories), which is a little obscure - it was expected to collapse, and so the fired chiefs pushed back media with their cameras several blocks, and when it finally collapsed, videos were shot from a distance, showing mostly only the upper part, and yes, it looked clean and straight down LIKE a controlled demolition.

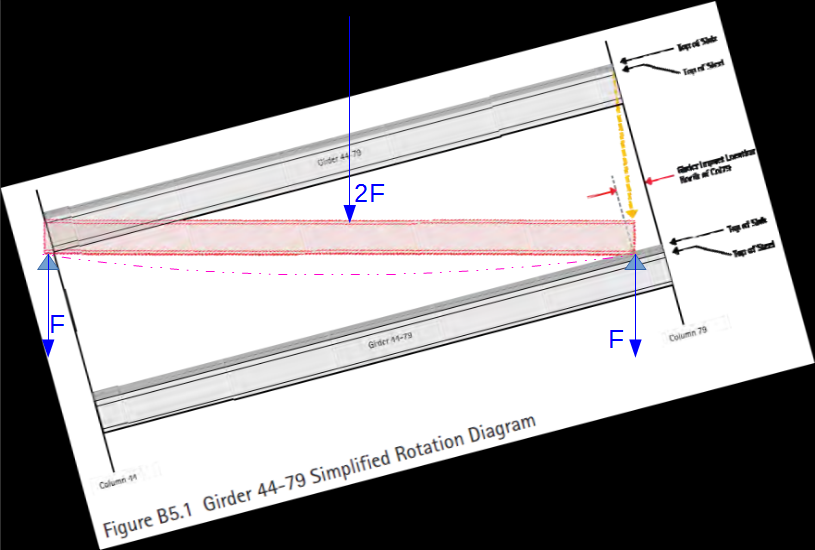
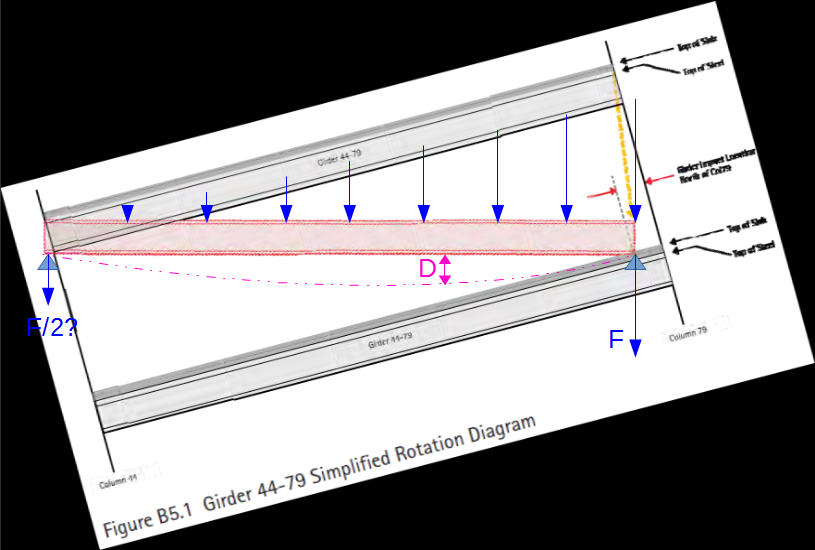
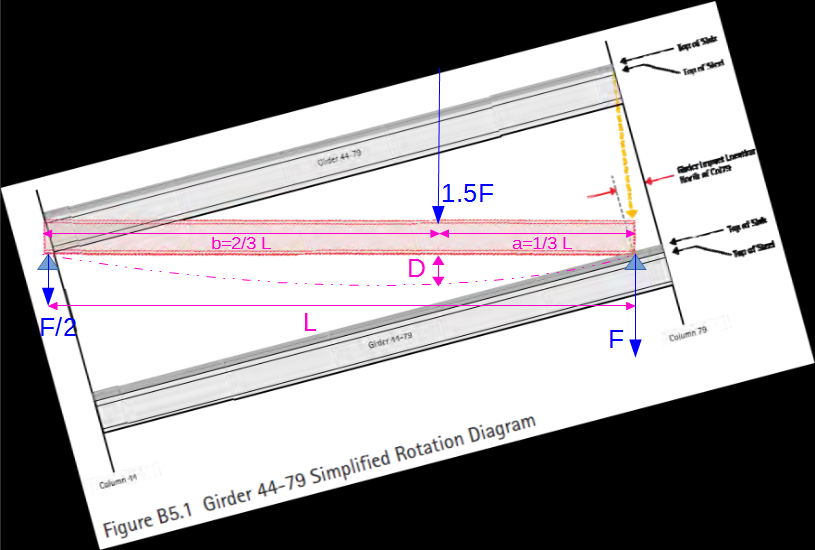
Fíres had been observed for several hours prior to the collapse primarily on floors 7 through 13, and the leading hypothesis is that the collapse initiated with the failing of the girder we are presently looking at. In short, the sequence was this:
  1. Fires on at least 6 floors made floor beams expand, bolts pop, stuff deform, and steel creak such that collapse was expected
  2. As I explained, expanding beams framing into "our" girder from the east on floor 13 pushed the girder towards west and off its seat on the internal column. Alternatively, it's also plausible that the cooling, somewhat buckled beams pulled the girder off towards east on the same column connection.
  3. The girder with beams and floor slabs it supported fell on the floor below, causing the corresponding connection there to fail. This happend progressively down to either the 5th floor (a strong mechanical floor), or even all the way to the ground
  4. This left the internal column (c79) unbraced on at least two sides over a span of 8 to 13 floors - it buckled
  5. Since column 79 was the largest column, supporting the largest floor area, the ensuing collapse of floor slabs all the way up to the roof quickly made neighboring two columns fail - as a result, a mechanical penthouse on the roof caved in - the first clear sign of collapse visible from outside.
  6. With a little delay, the rest of the core (which was more tightly framed than the first three columns) collapsed east to west
  7. This pulled floor beams spanning between core and perimeter columns down, and the peimeter columns inwards, particularly low in the buildig, right above a moment frame belt (floors 5-7)
  8. Perimeter columns buckled rapidly around floor 8, sending the walls straight down at practically free-fall for 2 seconds
Point #3 in this sequence is under scrutiny here: Would the falling girder really break the connection below?

This has been explored by a structural engineer, Guy Nordenson, who testified as expert witness on behalf of a group of insurance companies suing the developers, designers, builders and owners of the building for alleged negligence. Nordenson's report is available here:
https://www.metabunk.org/attachments/aegis-nordenson-expert-report-2-pdf.16785/
The actual technical report is pages 49 to 167 of the PDF document, and the particulars of the "falling girder impact" are in Appendix B on pages 210 to 254.

I have been discussing this with our Tony Szamboti and ozeco41/econ41 on Metabunk, here:
https://www.metabunk.org/does-the-e...alculations-demonstrate-anything.t7185/unread
(Other ISFers also participating)
I found myself at first in the rare situation that I was agreeing with the 9/11 Truther (Szamboti) and disagreeing with debunkers (econ41 and others), who didn't believe that the elasticity of the falling girder would affect the force on the connection below, OR believed that this was already, somehow, taken care off by Nordenson's model already.

I think agreement has been reached that the elasticity was in fact forgotten by Nordenson, but we have not yet agreed on numbers. Szamboti threw out two quick and dirty numbers, but I think he had them wrong both times, resulting in a "Truther-friendly" low stiffness which would make the connection survive and collapse arrest, and thus he claimed that Building 7 could not have collapsed like the official story claims and therefore we need a new investigation.

My result has the stiffness resulting in an impact force close enough to capacity to make failure possible but not certain.

And that is the relevance here: Would the collapse arrest or continue.


Szamboti's latest was that he plugged a model into his FEA software which gave him a natural frequency which he converted to a stiffness, and that stiffness results in a force about 1/3 of capacity - i.e. failure unlikely (post #192 and #200 on page 5 of the Metabunk thread).
However, I cannot vet his FEA model, and a factor of 3 is not so large that certain margins of error, particularly concerning the actual capacity after heating and deformations, could not change the outcome.
 
It is not the stiffness of the falling beam/girder that is a factor, but the impact loading of the mass of the falling beam on the (currently) intact beam.
Even if the stiffness of the falling beam were zero (A tub of lard/sand/water), the impact is still there, and extremely significant.
I have no clue WTF this is pertinent to.
 
rwguinn said:
It is not the stiffness of the falling beam/girder that is a factor, but the impact loading of the mass of the falling beam on the (currently) intact beam.
Even if the stiffness of the falling beam were zero (A tub of lard/sand/water), the impact is still there, and extremely significant.
I have no clue WTF this is pertinent to.
Click to expand...

The fact that the girder is elastic, and practically all its mass to the "left" (north) of the impact point, means that the load in the impact point gets dampened - read: decreased.

The "impact loading of the mass of the falling beam on the (currently) intact beam" is a function of the effective stiffness of both girders.

Nordenson, by not considering the elasticity, practically puts the stiffness of the falling girder at infinity (and considers only the stiffness of the intact one) - this maximizes the local load. Any stiffness less than infinity, including zero stiffness, implies a dampened/decreased load.

You say it would be "extremely significant" - it would be, in context, ONLY if the resulting force on the girder connection below is larger than, or at least in the the same ballpark as, the connection's vertical shear capacity. This is precisely what is being disputed here.

If it could be shown that the falling girder would not cause a cascading collapse of the floor bays, then the extant theory on why WTC7 collapsed is falsified.
 
Last edited:
rwguinn said:
It is not the stiffness of the falling beam/girder that is a factor, but the impact loading of the mass of the falling beam on the (currently) intact beam.
Even if the stiffness of the falling beam were zero (A tub of lard/sand/water), the impact is still there, and extremely significant.
I have no clue WTF this is pertinent to.
Click to expand...

As I now see, it is pertinent in someone's mind to conspiracy rubbish that uses junk engineering to justify some conspiracies. That was the joke assumption I made earlier, but now I see I was correct and the joke is reality.
 
Elind said:
As I now see, it is pertinent in someone's mind to conspiracy rubbish that uses junk engineering to justify some conspiracies. That was the joke assumption I made earlier, but now I see I was correct and the joke is reality.
Click to expand...

Whose mind would that be? And what conspiracy is being justified here? Who is the author of junk engineering here?
 
Oystein said:
Whose mind would that be? And what conspiracy is being justified here? Who is the author of junk engineering here?
Click to expand...

Did I not see you saying that you thought the conspiracy theories had merit. As to the stiffness issue, it has already been commented by others that the stiffness is essentially irrelevant to the effect of a falling beam on the one below it.
 
Oystein said:
This in turn is equivalent (?) to a point load 1/3 L from the free end:



By the usual laws of levers, a load of 3/2 is distributed 1/2 : 1 to the ends.

The stiffness formula for such an off-center loaded beam is
K2/3 = 3*E*I*L / (a2 * (L-a)2)
where a = 1/3 L, so
K2/3 = 3*E*I*L / ((1/3 L)2 * (2/3 L)2) = 3*E*I*L / (4/81 L4) = 243/4 E*I / L^3

This looks weird - I am not too confident my derivation is error-free :o
Click to expand...
Why is there 0.5F at the left, hinged side? Is that simple mass of the girder load on the hinge? There's no angular momentum at the hinge point as it doesn't move.
 
You must log in or register to reply here.

Back
Top Bottom