• Quick note - the problem with Youtube videos not embedding on the forum appears to have been fixed, thanks to ZiprHead. If you do still see problems let me know.

Special Relativity math question, thanks in advance again

Skeptic Ginger

Nasty Woman
Skeptic Ginger
Joined
Feb 14, 2005
Messages
96,955
If a spaceship traveled at 1/10th the speed of light for 40 years, how much time would have passed on Earth during that same time?

Thanks
 
[latex]$\frac{40}{\sqrt{1-(1/10)^2}} \approx 40.20[/latex]
Under the conventional definition of simultaneity in SR. If the spaceship returns to Earth at that time, there's no ambiguity about it.

ETA: I should probably explain the ambiguity if the ship doesn't come back: do you mean how much time has elapsed on Earth in the Earth-stationary frame or how much time has elapsed on Earth in the spaceship-stationary frame? Those have different answers because of relativity of simultaneity, i.e., they will disagree as to which event on Earth is simultaneous with "40 years have passed on the ship."
 
Last edited:
So it's only when you get much closer to light speed then that a significant difference would occur?
 
Yes, how much the Lorentz gamma [latex]$\frac{1}{\sqrt{1-(v/c)^2}}$[/latex] differs from 1 is a good indicator as to how important relativistic effects are. Or, for low v, (1/2)(v/c)². So, for 1/10th the speed of light, you can expect the answers change by one part in 200.
 
Weird, if I use that formula with 9/10th the speed of light I only get ~93.2 years lapsing on Earth in that 40 years. I always thought you'd end up much further in the future on Earth.

Maybe I have something else conceptually wrong. If you traveled at 1/2 the speed of light for 40 Earth years, how long would it feel like had passed to the humans on the spaceship? Wouldn't they feel like 40 years passed and not be subject to the speed from within the ship?
 
Last edited:
Gamma is heavily skewed toward speeds very near c. Start adding extra 9's to your decimal (.99c, .999c, .9999c) and see what happens to your time dilation.
 
AvalonXQ said:
Gamma is heavily skewed toward speeds very near c. Start adding extra 9's to your decimal (.99c, .999c, .9999c) and see what happens to your time dilation.
Click to expand...
OK that's weird. At .9999 c i get ~2857 years.

Now I'm confused. I rechecked the time with .9c I still get ~92 years. A logarithmic curve I take it? I'm trying to conceptualize what is going on.
 
Last edited:
But if time distortion is minimal until you get really close to c, that makes my problem much easier to deal with. So, oh well, the Universe is what it is.
 
Skeptic Ginger said:
Weird, if I use that formula with 9/10th the speed of light I only get ~93.2 years lapsing on Earth in that 40 years. I always thought you'd end up much further in the future on Earth.
Click to expand...
Slightly less than that (I get a bit less than 92 years), but close enough. As AvalonXQ says, it's asymptotic at lightspeed, so it grows crazy fast there.
99.0%: x7.09
99.9%: x22.4

Skeptic Ginger said:
Now I'm confused. I rechecked the time with .9c I still get ~92 years. A logarithmic curve I take it? I'm trying to conceptualize what is going on.
Click to expand...
It's not logarithmic, but it is asymptotic like log near 0. It reaches infinity at finite speed.
500px-Lorentz_factor.svg.png
 
Last edited:
I did get 92 the second time, don't know how I got 93. Post #9:
I rechecked the time with .9c I still get ~92 years
Click to expand...
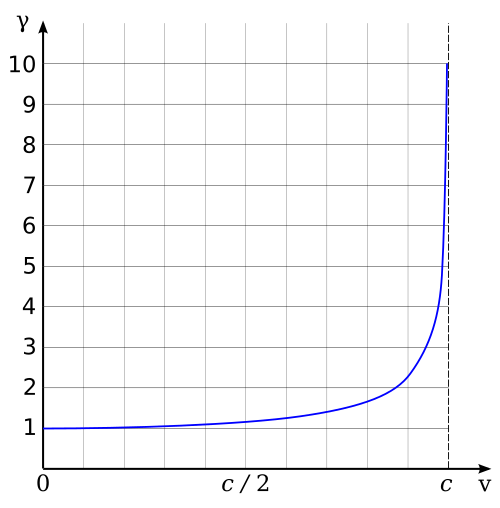
Apparently I didn't even notice I had two different answers. I'd be a failure as a CPA. :p

So would the people traveling within the ship feel like 40 years went by (the OP problem)?
 
Skeptic Ginger said:
So would the people traveling within the ship feel like 40 years went by (the OP problem)?
Click to expand...

Yes. People in the ship would experience 40 years within the ship. If they kept in communications contact with Earth, though, they could realize that 92 years actually went by.
 
Skeptic Ginger said:
So would the people traveling within the ship feel like 40 years went by (the OP problem)?
Click to expand...

Yup.

And you might want to figure out just how much frickin' energy it takes to get an object going that fast. Having done that, you might realize how far outside our everyday experience you have to get, in order for relativistic effects to become noticeable (in the everyday sense).
 
WhatRoughBeast said:
Yup.

And you might want to figure out just how much frickin' energy it takes to get an object going that fast. Having done that, you might realize how far outside our everyday experience you have to get, in order for relativistic effects to become noticeable (in the everyday sense).
Click to expand...
There are some things the readers of the story are just going to have to take on face value but i was only going for .1c, nothing close to .9c.

I was going to stretch reality just a bit: ;)

http://www.universetoday.com/15403/how-long-would-it-take-to-travel-to-the-nearest-star/:
Nuclear pulse propulsion is a theoretically possible form of fast space travel. Very early on in the development of the development of the atomic bomb, nuclear pulse propulsion was proposed in 1947 and Project Orion was born in 1958 to investigate interplanetary space travel. In a nutshell, Project Orion hoped to harness the power of pulsed nuclear explosions to provide a huge thrust with very high specific impulse. It is a major advantage to extract maximum energy from a spacecraft’s fuel to minimize cost and maximize range, therefore a high specific impulse creates faster, longer-range spaceflight for minimum investment....

.... it would take a Project Orion-type craft approximately 85 years to travel from the Earth to Proxima Centauri.
Click to expand...
 
Skeptic Ginger said:
So would the people traveling within the ship feel like 40 years went by (the OP problem)?
Click to expand...

If 40 years subjective time for people on the ship is what you meant then yes. If you meant 40 years subjective time for us on Earth then no. There is, of course, no objective time.

I think there's a need to allow for us on Earth being in Earth's gravitational field (and the Sun's, and Jupiter's, and ...) when calculating the time-difference. I'm no expert, though.
 
You must log in or register to reply here.

Back
Top Bottom