[Continuation] Why James Webb Telescope rewrites/doesn't the laws of Physics/Redshifts (2)

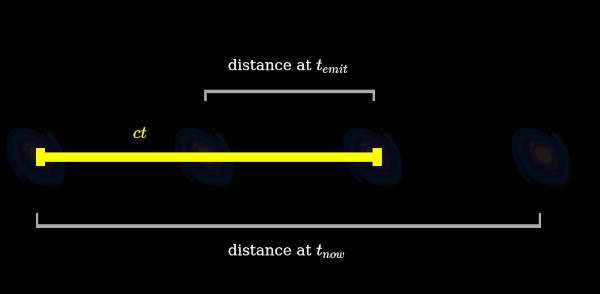
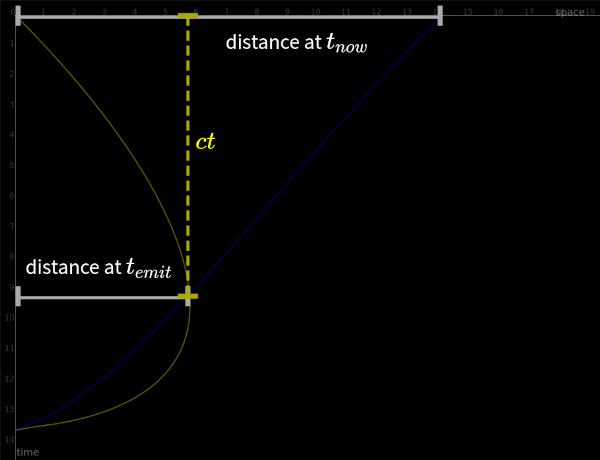
[W.D.Clinger]

Right. The only change I made was to update distances using v=c/(1+z), without changing the lines of code that update z and H.

You changed the line of code that applies H to the model.

You could set it to H = "Clinger Was Here" and it wouldn't make a lick of difference

The highlighted statement is flat-out false. Readers can decide for themselves whether it was a deliberate lie, or just another indication that Mike Helland doesn't understand his own algorithm.

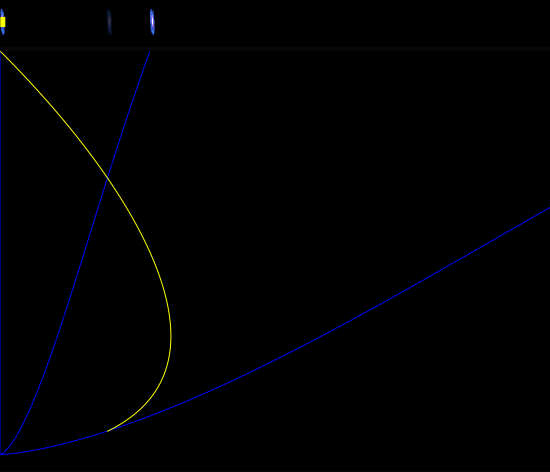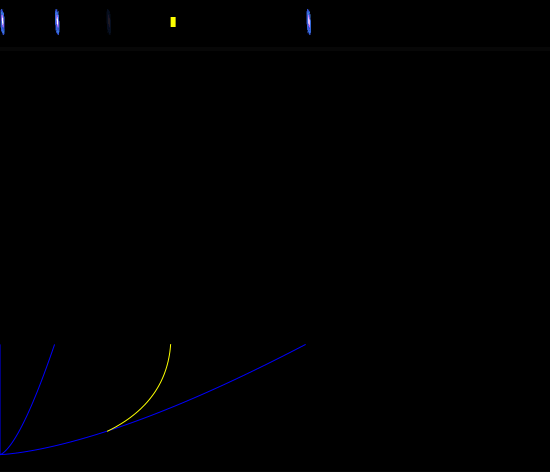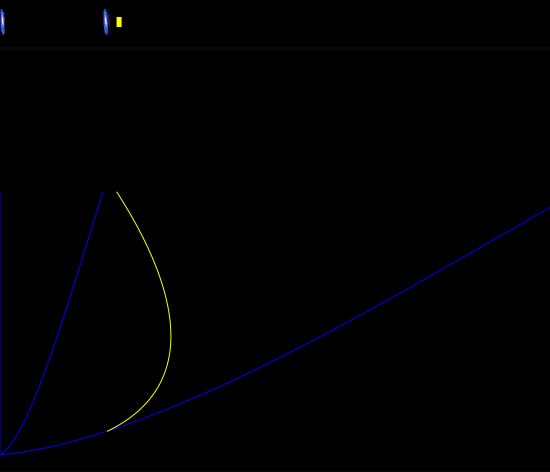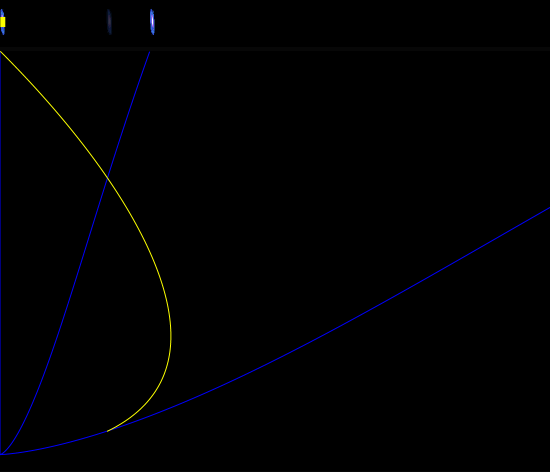
Here is the body of Mike Helland's while loop after I modified it. The "if useHX" code is Mike Helland's original code. The "if not useHX" code is the result of changing the two lines of code that update distances. It should be obvious that I never changed a "line of code that applies H to the model", because (apart from the two lines that update distances) there never was such a line of code.

    t -= 1
    if useHX:
        x1 += c - H * x1
        x += c - H * x
        z = 0.1 / (x1 - x) - 1
    if not useHX:
        x1 += c / (1 + z)
        x += c / (1 + z)
        z = 0.1 / (x1 - x) - 1
    H = H0 * (OmegaM * (1+z)**3 + OmegaL + OmegaK * (1+z)**2)**0.5

His algorithm breaks because it is more fragile than the bog-standard algorithm. The bog-standard algorithm does not break if we make precisely and only the change from v=c−Hd to v=c/(1+z).

Your "bog-standard" code is also updating the reference distance using H. Of course it works.

The spoiler immediately below shows Scheme code for the system derivative that uses v=c−Hd, followed by the code for the system derivative that uses v=c/(1+z). It should be obvious that the only changes are to the derivatives used to update x1 and x2. Those changes correspond exactly to the changes I made to Mike Helland's Python code, as shown above.

Here is the system derivative for the bog-standard algorithm using v=c−Hd:

  (lambda (state)
    (let ((a (vector-ref state 0))
	  (x1 (vector-ref state 1))
	  (x2 (vector-ref state 2)))
      (let* ((z (- (/ 1.0 a) 1.0))
	     (H (* H0 (sqrt (+ (* OmegaM (expt (+ 1.0 z) 3.0)) OmegaL)))))
        (vector [color=green](- (* H a))[/color]
		[color=blue](- c (* H x1))[/color]
		[color=blue](- c (* H x2))[/color])))))

Note that neither x1 nor x2 affect the computation of a, z, or H. The distances x1 and x2 appear in the above code only because they were present in Mike Helland's original code, where they were used to update z.

Here is the system derivative for the bog-standard algorithm using v=c/(1+z):

  (lambda (state)
    (let ((a (vector-ref state 0))
	  (x1 (vector-ref state 1))
	  (x2 (vector-ref state 2)))
      (let* ((z (- (/ 1.0 a) 1.0))
	     (H (* H0 (sqrt (+ (* OmegaM (expt (+ 1.0 z) 3.0)) OmegaL)))))
        (vector [color=green](- (* H a))[/color]
		[color=blue](/ c (+ 1.0 z))[/color]
		[color=blue](/ c (+ 1.0 z))[/color])))))

It should be obvious that no changes were made to the derivative for a (highlighted in green). The only changes that were made were to the derivatives for the distances (highlighted in blue).

With those changes, the Scheme code continues to work correctly for models with constant H.

With exactly those same changes, Mike Helland's Python code breaks.

Those changes break Mike Helland's algorithm because that algorithm uses x1-x2 to update z instead of using the scale factor.

That's the only significant difference between Mike Helland's algorithm and the bog-standard algorithm, and it is precisely that difference that has served as the basis for Mike Helland's almost daily claim that his algorithm is more general and easier to understand than the bog-standard algorithm.

Mike Helland now admits that his algorithm doesn't work with v=c/(1+z) unless we also change the part of his algorithm that he's been most proud of.

I hope no one is failing for your antics this time.

It seems Mike Helland is falling for his own antics.

That "significant change" just ensures that the value of H still affects the results of the model.

You significantly changed it by removing it from the model.

Let's note once again that no such change was needed when I modified the bog-standard algorithm to use v=c/(1+z) instead of v=c−Hd (for models with constant H).

But Mike Helland's algorithm breaks if we use v=c/(1+z) instead of v=c−Hd. To repair that breakage, it is necessary to make a significant change to Mike Helland's algorithm. To be precise, we must replace the very aspect of Mike Helland's algorithm that Mike Helland has been touting as superior to the bog-standard algorithm.

 

[Mike Helland]

Here is the body of Mike Helland's while loop after I modified it. The "if useHX" code is Mike Helland's original code. The "if not useHX" code is the result of changing the two lines of code that update distances. It should be obvious that I never changed a "line of code that applies H to the model", because (apart from the two lines that update distances) there never was such a line of code.

    t -= 1
    if useHX:
        x1 += c - H * x1
        x += c - H * x
        z = 0.1 / (x1 - x) - 1
    if not useHX:
        x1 += c / (1 + z)
        x += c / (1 + z)
        z = 0.1 / (x1 - x) - 1
    H = H0 * (OmegaM * (1+z)**3 + OmegaL + OmegaK * (1+z)**2)**0.5

The spoiler immediately below shows Scheme code for the system derivative that uses v=c−Hd, followed by the code for the system derivative that uses v=c/(1+z). It should be obvious that the only changes are to the derivatives used to update x1 and x2. Those changes correspond exactly to the changes I made to Mike Helland's Python code, as shown above.

It's plain as day.

The "useHX" code path reads the value of H.

The "not useHX" code path doesn't.

You're setting the value of H, sure, but you're never reading it. It's value has no effect on the results.

Here is the system derivative for the bog-standard algorithm using v=c/(1+z):

  (lambda (state)
    (let ((a (vector-ref state 0))
	  (x1 (vector-ref state 1))
	  (x2 (vector-ref state 2)))
      (let* ((z (- (/ 1.0 a) 1.0))
	     (H (* H0 (sqrt (+ (* OmegaM (expt (+ 1.0 z) 3.0)) OmegaL)))))
        (vector [color=green](- (* H a))[/color]
		[color=blue](/ c (+ 1.0 z))[/color]
		[color=blue](/ c (+ 1.0 z))[/color])))))

It should be obvious that no changes were made to the derivative for a (highlighted in green). The only changes that were made were to the derivatives for the distances (highlighted in blue).

It should also be obvious that - (* H a) reads the value of H and its value effects the results.

It should also be obvious that you've broken the algorithm for every model except dS, so what business this algorithm has calculating H is beyond me.


Let's recapp.

I said v=c-Hd is the speed of light, and provided an algorithm that solves it, and consequently all observables in FLRW.

I also said that, if H is constant, you can simplify if to just use x instead of x and x2 or x and a.

You can get away with this because z = c/(c - Hd) - 1. So you're gonna need that if you simplify for dS.

You took v=c-Hd out of the algorithm, both in the moving of the photon and in the calculating of redshift, and showed that it doesn't work without it.

Your algorithm still works because you've abstracted the -Hd to a reference distance "a."

 

[Mike Helland]

The "if not useHX" code is the result of changing the two lines of code that update distances. It should be obvious that I never changed a "line of code that applies H to the model", because (apart from the two lines that update distances) there never was such a line of code.

You just said that you changed the two lines of code that update distance using H to not use H.

Then you said you never changed a line of code that applies H to the model, after just admitting you did, and then you claimed those lines don't exist, except for the ones that did.

I'm not trying to embarrass you here, but maybe it's been a long day?

 

[W.D.Clinger]

ETA:

The following remark reveals profound ignorance of FLRW models.

Your algorithm still works because you've abstracted the -Hd to a reference distance "a."

The scale factor a(t) is not a distance.

The redshift z(t) and Hubble parameter H(t) are defined in terms of the scale factor a(t).

By telling us he thinks the scale factor is a distance, Mike Helland is telling us he doesn't actually understand the definitions of redshift and the Hubble parameter.​

Here is the body of Mike Helland's while loop after I modified it. The "if useHX" code is Mike Helland's original code. The "if not useHX" code is the result of changing the two lines of code that update distances. It should be obvious that I never changed a "line of code that applies H to the model", because (apart from the two lines that update distances) there never was such a line of code.

    t -= 1
    if useHX:
        x1 += c - H * x1
        x += c - H * x
        z = 0.1 / (x1 - x) - 1
    if not useHX:
        x1 += c / (1 + z)
        x += c / (1 + z)
        z = 0.1 / (x1 - x) - 1
    H = H0 * (OmegaM * (1+z)**3 + OmegaL + OmegaK * (1+z)**2)**0.5

The spoiler immediately below shows Scheme code for the system derivative that uses v=c−Hd, followed by the code for the system derivative that uses v=c/(1+z). It should be obvious that the only changes are to the derivatives used to update x1 and x2. Those changes correspond exactly to the changes I made to Mike Helland's Python code, as shown above.

It's plain as day.

The "useHX" code path reads the value of H.

The "not useHX" code path doesn't.

You're setting the value of H, sure, but you're never reading it. It's value has no effect on the results.

That's exactly right.

Mike Helland thought he was being clever when he used x1-x2 to update z, and touted that misfeature of his algorithm as a significant improvement upon the bog-standard algorithm. In particular, Mike Helland claimed his algorithm was more general and easier to understand than the bog-standard algorithm.

In reality, Mike Helland's use of x1-x2 to update z made his algorithm less general and harder to understand than the bog-standard algorithm.

That became obvious when we modified the Helland and bog-standard algorithms to use v=c/(1 + z) instead of v=c−Hd for FLRW models with constant Hubble parameter H.

With the bog-standard algorithm, that modification was confined to the lines of code that update x1 and x2.

With Mike Helland's algorithm, confining that modification to the lines of code that update x1 and x2 breaks the algorithm. To repair that breakage, we must replace the very aspect of Mike Helland's algorithm that Mike Helland has been bragging about.

Here is the system derivative for the bog-standard algorithm using v=c/(1+z):

  (lambda (state)
    (let ((a (vector-ref state 0))
	  (x1 (vector-ref state 1))
	  (x2 (vector-ref state 2)))
      (let* ((z (- (/ 1.0 a) 1.0))
	     (H (* H0 (sqrt (+ (* OmegaM (expt (+ 1.0 z) 3.0)) OmegaL)))))
        (vector [color=green](- (* H a))[/color]
		[color=blue](/ c (+ 1.0 z))[/color]
		[color=blue](/ c (+ 1.0 z))[/color])))))

It should be obvious that no changes were made to the derivative for a (highlighted in green). The only changes that were made were to the derivatives for the distances (highlighted in blue).

It should also be obvious that - (* H a) reads the value of H and its value effects the results.

That's exactly right (apart from the misspelling of "affects").

The bog-standard algorithm solves the differential equation

da/dt = H(t) a(t)​

and uses that solution to drive all auxiliary calculations.

Mike Helland thinks it's better to use his ad hoc technique for updating z, in which x1−x2 serves as a proxy for the scale factor a(t).

But it isn't better. Most of the calculations we'd want to perform don't involve those particular distances x1 and x2 at all, making them extraneous. Mike Helland's algorithm has to compute x1 and x2 even when they are conceptually irrelevant to the calculation we want to perform.

Furthermore, the x1−x2 hack doesn't even work when, for a model with constant H, we replace v=c−Hd by v=c/(1+z). To repair the algorithm, we have to reintroduce v=c−Hd into the calculation of z. So we can't fully replace v=c−Hd by v=c/(1+z) in Mike Helland's algorithm.

With the bog-standard algorithm, we can fully replace v=c−Hd by v=c/(1+z).

That demonstrates the greater generality of the bog-standard algorithm.

The fact that Mike Helland still doesn't understand the above argues against his claim that the Helland algorithm is easier to understand.

It should also be obvious that you've broken the algorithm for every model except dS, so what business this algorithm has calculating H is beyond me.

The bog-standard algorithm calculates H because the bog-standard algorithm solves the differential equation

da/dt = H(t) a(t)​

Although H(t) is constant for the de Sitter (dS) model, a(t) is not constant, so the value of H(t) is needed at each step to calculate the value of (da/dt)(t).

In what he wrote above, Mike Helland is saying he doesn't understand why the bog-standard algorithm calculates H at each step even for the extremely special case of a model in which H is constant.

Which is just a way of saying Mike Helland doesn't understand why people prefer general-purpose algorithms that work with an extremely wide range of model parameters, instead of developing and coding a new special-purpose algorithm for every special case of model parameters.

Let's recapp.

To recap:

If Mike Helland were a better programmer, he would understand why people prefer general-purpose software to a plethora of special-purpose software.​

 

[Mike Helland]

If Mike Helland were a better programmer, he would understand why people prefer general-purpose software to a plethora of special-purpose software.

You're out of your depth in that swimming pool, amigo.

Your "general purpose" algorithm is broken for all models except dS, and contains superfluous code at that.


The algorithm works like this:

* update d based on Hd
* update z based on d
* update H based on z

That works for all FLRW.

For an FLRW with a constant expansion rate, you can do that, or you can do:

* update d based on z
* update z based on Hd
* update H based on z

What you can't do is:

* update d based on z
* update z based on d
* update H based on z

It makes H obsolete.

In an expanding universe, photons become redshifted. But they also arrive at a reduced rate, known as time dilation.

In an exponentially expanding universe (aka, constant expansion rate, aka de Sitter (dS), asks pure dark energy [OmegaL=1, OmegaM=0]) the "low redshift approximations" become the actual results of the model.

Which can be found by setting E(z) to 1 in the respective integrals and solving analytically:

* comoving distance

http://latex.codecogs.com/gif.latex?d_C = \frac{c}{H_0} \int_0^z \frac{dz'}{E(z')} = \frac{c}{H_0} z​

* angular diameter distance

http://latex.codecogs.com/gif.latex?d_A = \frac{d_C}{1+z} = \frac{c}{H_0} \frac{z}{1+z}​

* light travel time

http://latex.codecogs.com/gif.latex?t = \frac{1}{H_0} \int_0^z \frac{dz'}{(1+z)E(z')} = \frac{c}{H_0} \log (1+z)​

You can see why those FLRW parameters results in E(z) = 1 by looking at E(z):

http://latex.codecogs.com/gif.latex?E(z) = \sqrt{\Omega_m (1+z)^3 + \Omega_\Lambda}​

When http://latex.codecogs.com/gif.latex?\Omega_m =0, \Omega_\Lambda = 1, you can see why a pure dark energy universe has a constant expansion rate, because:

http://latex.codecogs.com/gif.latex?H(z) = H_0 E(z)​

With those integrals, you can calculate every observable with FLRW, including cosmic redshift and cosmic time dilation.

You can also generalize all those integrals into v=c-Hd, and solve with my algorithm.

Due to time dilation if photons were emitted 1 second apart from z=1, they would arrive at z=0 two seconds apart.

This is logical and easily visually apparent by analyzing my algorithm. First consider the version that goes forward in time.

You see the left photon travels at c (because c+Hd = c when d=0) from t=0 to t=1, but the right photon is traveling faster, because its d > 0. In the second step, the left photon is now traveling as fast as the first right one was, but now the right one is traveling is faster. This will continue on and one.

This means that successive photons get farther apart, being observed as time dilation.

You should note that the time dilation here cannot be reproduced by the relativistic Doppler effect. As an example.

At z =1 in dS, the galaxy is at c/H₀ now, moving at v=c.

When its light was emitted, it was at 0.5 c/H₀, moving at c/2 (both the galaxy and its light, but in opposite directions).

This means a photon emitted by the galaxy 1 second after the previous photon will only be 0.5 light seconds behind due to the recession velocity, or 1.5 seconds in total.

However the photon shows up 2 seconds later, not 1.5. So the effect is not relativistic Doppler, which breaks down at v=c anyways.

If some courageous soul thinks W.D.Clinger's variation of my algorithm more clearly represents reality, please explain how this:

Shows us time dilation.

Notice that H is always positive, and always stays positive in LCDM. Using v=c+Hd the photon never be moving in the opposite direction of where it really wants to go.

This means you can never have an angular diameter turnaround if you tried calculating LCDM forward in time from a starting point in time prior to the angular diameter turnaround.

This is means it is impossible to calculate LCDM (or any non-dS FLRW model) where time moves forward from a starting time prior to z=1.6.

Unless you use comoving coordinates, in which case your starting conditions already include the future.

 

[W.D.Clinger]

If Mike Helland were a better programmer, he would understand why people prefer general-purpose software to a plethora of special-purpose software.

You're out of your depth in that swimming pool, amigo.

Your "general purpose" algorithm is broken for all models except dS, and contains superfluous code at that.

The general-purpose algorithm is the algorithm that solves for the scale factor a(t) in any FLRW model. That gives you z(t) and H(t) and everything else that can be defined in terms of the scale factor. It is also easy to attach code that calculates other things such as distances and the evolution of mass-energy density and pressure.

Modifying that general-purpose algorithm to use v=c/(1+z) does indeed break it for all models in which the Hubble parameter H(t) changes over time, but that's true of the Helland algorithm(s) as well.

Mike Helland's apparent belief that dS is the only model with constant H(t) is yet another sign of his ignorance of FLRW models.

Notice that H is always positive, and always stays positive in LCDM.

That is false. LCDM includes all FLRW models. Everyone who understands LCDM and FLRW models is aware of FLRW models that start with a Big Bang and end with a Big Crunch.

But Mike Helland thinks H(t) is always positive and cannot go negative.

This is means it is impossible to calculate LCDM (or any non-dS FLRW model) where time moves forward from a starting time prior to z=1.6.

That sentence is nonsense.

Unless you use comoving coordinates, in which case your starting conditions already include the future.

We can add comoving coordinates to the already long list of things Mike Helland is telling us he doesn't understand.

 

[Mike Helland]

The general-purpose algorithm is the algorithm that solves for the scale factor a(t) in any FLRW model.

Agreed.

That gives you z(t) and H(t) and everything else that can be defined in terms of the scale factor.

Alternatively, one that gives you distance, time, and redshift, since the scale factor is just 1/(1+z).

Were we to have never defined cosmological phenomena in terms of wavelength, ie redshift z, and instead in terms of frequency and energy, ie, negative blueshift, we wouldn't be having this argument.

If:

http://latex.codecogs.com/gif.latex?1+b = \frac{1}{1+z} = \frac{f_{obs}}{f_{emit}}

In FLRW, 1+b would be the scale factor. 1+b = a

In dS, angular diameter distance would be r = -bc/H₀.

Put like this, the concepts of "redshift" and "scale factor" are literally the difference between b and 1+b.

I get that already knowing the ins and outs of FLRW (and thank you for teaching me), which is why the scale factor is so great, but it's just wavelength emitted over wavelength observed.

Modifying that general-purpose algorithm to use v=c/(1+z) does indeed break it for all models in which the Hubble parameter H(t) changes over time, but that's true of the Helland algorithm(s) as well.

Yes. You took working code and broke it. I think we can move past that.

Mike Helland's apparent belief that dS is the only model with constant H(t) is yet another sign of his ignorance of FLRW models.

What else? Assuming H₀ > 0.

That is false. LCDM includes all FLRW models. Everyone who understands LCDM and FLRW models is aware of FLRW models that start with a Big Bang and end with a Big Crunch.

I think you might need to take a rest for the day because you should know this better.

LCDM is a specific set of parameters for FLRW.

So FLRW includes LCDM.

FLRW includes models with and without dark energy and models with and without matter.

LCDM includes dark energy (L, about 70%) and matter (CDM, about 30%). Without those it wouldn't be LCDM.

All models except pure L have a big bang. Some models collapse. Some, like ours, don't.

But Mike Helland thinks H(t) is always positive and cannot go negative.

Between now and big bang?

It's positive.

 

[W.D.Clinger]

LCDM is a specific set of parameters for FLRW.

Yes.

Or rather, sort of. As elaborated below, LCDM is a specific set of parameters, but several of those LCDM parameters do not correspond to any FLRW parameters.

So FLRW includes LCDM.

No. Not all of the six independent parameters of the LCDM model are parameters of a pure FLRW model.

It goes the other way. All FLRW parameters can be found among the independent and derived parameters of the LCDM model, but not all parameters of the LCDM model are FLRW parameters.

In particular, the H₀, Ω_M, and Ω_Λ that have been so prominent in the recent history of this thread are derived parameters of the LCDM model.

From that it follows that (almost!) every FLRW model is also an LCDM model, but not every LCDM model is an FLRW model. In fact, most LCDM models are not pure FLRW models.

For some values of the FLRW parameters that are permitted by the LCDM theory, the FLRW model determined by those parameters ends in a Big Crunch. The Hubble parameter H(t) goes negative as the model approaches that Big Crunch.

FLRW includes models with and without dark energy and models with and without matter.

And since (almost!) every FLRW model is an LCDM model, LCDM includes models with and without dark energy and with and without matter.

LCDM includes dark energy (L, about 70%) and matter (CDM, about 30%). Without those it wouldn't be LCDM.

The values of those parameters are not hard-wired into LCDM. Their values are estimated from empirical measurements and associated theory.

Mike Helland cannot insist that the empirically determined values of those parameters are so well known as to rule out a Big Crunch without conceding that the values of those parameters are so well known as to rule out a non-expanding universe.

In other words, Mike Helland is digging himself a hole. He cannot argue that the empirically determined values of LCDM parameters rule out a Big Crunch without conceding that Helland physics is toast.

All models except pure L have a big bang.

That is the source of the only exceptions I know of to the general rule that every FLRW model is an LCDM model. One of the LCDM model's independent parameters is the age of the universe, and the LCDM model assumes that parameter is some finite age.

That rules out all FLRW models that don't have a Big Bang. Note well that one of the models it rules out is what Mike Helland calls the "pure L" model.

Some models collapse.

Here Mike Helland is admitting that some LCDM models end in a Big Crunch.

Some, like ours, don't.

But with that sentence he is saying he is convinced the empirical evidence proves to his satisfaction that our universe began with a Big Bang, has been expanding ever since, and will continue to expand forever.

In other words, Mike Helland is admitting that Helland physics is toast.

It gives me great pleasure to congratulate the author and sole proponent of Helland physics on his unequivocal rejection of Helland physics.

 

[Mike Helland]

LCDM includes models with and without dark energy and with and without matter.

Lambda-CDM doesn't insist on there being a Lambda and a CDM?

Seems pedantic either way. We have our algorithms for FLRW.

Mine's the most general because it does flat, open and closed.

Mike Helland cannot insist that the empirically determined values of those parameters are so well known as to rule out a Big Crunch without conceding that the values of those parameters are so well known as to rule out a non-expanding universe.

In other words, Mike Helland is digging himself a hole. He cannot argue that the empirically determined values of LCDM parameters rule out a Big Crunch without conceding that Helland physics is toast.

I'm not familiar with how they are empirically determined.

I mean, a little. It's those spikes on the multipole moment graph, right?

I keep trying to dive deeper into that. Still not totally sure what a multipole moment is and how it relates to the CMB,

 

[Mike Helland]

Lambda-CDM doesn't insist on there being a Lambda and a CDM?

Seems pedantic either way. We have our algorithms for FLRW.

Mine's the most general because it does flat, open and closed.



I'm not familiar with how they are empirically determined.

I mean, a little. It's those spikes on the multipole moment graph, right?

I keep trying to dive deeper into that. Still not totally sure what a multipole moment is and how it relates to the CMB,

These guys explain a lot about this, covering more in and outs than just about any other explanation I've found:

https://www.youtube.com/watch?v=aNkSXUlz6YI&list=PLp9GASrf6rzns9Qr8HJ7Hq7g8ao8wu2S8&index=1

 

[Ziggurat]

That's pretty much what I'm doing, except I didn't think the equation was an integral (at least not a simple one) and the answers involved more than the area under the curve (which I suppose in this case would distance, taking a velocity * time as the rectangle box?)

That's because you don't really understand calculus. What do you think an integral is? What do you think a differential equation is? Solving a differential equation IS integration. It's not written with an integral symbol, because you're generally not doing a definite integral when you solve a differential equation, but mathematically you're doing the exact same thing.

The thing is, if that equation allows one calculate so much so easily, why wouldn't anyone teach it?

What the actual **** are you even talking about? I just pointed you to several tutorials. I learned it myself in school. Hell, I used to teach it. It's taught all the bloody time. It's only novel to you because you never actually studied this stuff.

I'm not claiming to have invented any new mathematical technique. Because, yes, this is just a stepwise Euler method of numerically integrating a differential equation. I get that now.

Do you really? I remain skeptical.

But the one differential equation, and the algorithm that solves it, makes quicker work of an FLRW model than the handful of integrals in the texts.

And it seems it only requires middle school maths to comprehend.

Quite so. Which is why nobody ever bothered explicitly writing it out, because EVERYONE doing actual work on cosmology would already know how to trivially go from the integral to a numerical solution to that integral without anyone having to hold their hand. And they could do it in whatever language they felt convenient, or even just in a spreadsheet. This is the same reason nobody writes out the manual long division solution if a number is divided by another number: everyone knows how to do it, there's no need to show it.

 

[Mike Helland]

What the actual **** are you even talking about? I just pointed you to several tutorials. I learned it myself in school.

The equation, v=c-Hd?

 

[Mike Helland]

That's because you don't really understand calculus. What do you think an integral is? What do you think a differential equation is? Solving a differential equation IS integration. It's not written with an integral symbol, because you're generally not doing a definite integral when you solve a differential equation, but mathematically you're doing the exact same thing.

Understood.

I produced my algorithm (with the changing expansion rate) during our discussion about time dilation. My primary concern was the time in between two photons arriving.at an observer.

That's why my solution tracks two photons separated by an initial distance.

Translating that to a system of integrals was a total nightmare. I figured it was kind of like one of those simple CA's that produces seemingly random (but just complex) results. The kind of simple rules that are nice for algorithms but not for equations. I thought my solution was verging on that territory.

W.D.Clinger added a nice little abstraction, taking the initial distance that separates the photons out and treating it separately. So instead of two photons separated by a distance, you just have one photon and a reference distance.

Now instead of subtracting the distance between the two photons, you're judging the offset distance from observer, so you don't have to subtract by zero, which neatens up the equations, compared to the mess I had developed.

 

[Mike Helland]

The equation, v=c-Hd?

Cranking up the Cunningham dial:

https://www.youtube.com/watch?v=aLyx4aDocaE

 

[Mike Helland]

Here are four ways to quantify redshift, where http://latex.codecogs.com/gif.latex?\lambda is a wavelength:

http://latex.codecogs.com/gif.latex?a = \frac{\lambda_{emit}}{\lambda_{obs}}

http://latex.codecogs.com/gif.latex?1 + b = \frac{\lambda_{emit}}{\lambda_{obs}}

http://latex.codecogs.com/gif.latex?1 - r = \frac{\lambda_{emit}}{\lambda_{obs}}

http://latex.codecogs.com/gif.latex?1 + z = \frac{\lambda_{obs}}{\lambda_{emit}}​

These are all fundamentally the same. The only real difference is the numeric range redshfits fall in for each.

http://latex.codecogs.com/gif.latex?0 < a < 1

http://latex.codecogs.com/gif.latex?-1 < b < 0

http://latex.codecogs.com/gif.latex?0 < r < 1

http://latex.codecogs.com/gif.latex?0 < z < \infty​

Any of these are valid choices, to be used as the value we record when we measure redshift, or in our equations.

z is kind of nice because things are spread out instead of crammed between 0 and 1 or -1.

But z doesn't relate to distance very well, unlike the others. For the most part, in a big bang universe, z=1 is around half way back to the beginning. So half is between 0 and 1, the other half between 1 and infinity.

Notice you never see "z" alone. It has one exact use, as the comoving distance in a de Sitter model, d = cz/H, otherwise it is a mere low redshift approximation.

Everywhere else it appears is as 1+z or its inverse.

For this reason, "a" is pretty useful in the equations, and is more or less the de factor way to reason about redshifts.

From

ΛCDM Cosmology for Astronomers

https://arxiv.org/pdf/1804.10047.pdf

Because 1 ≤ (1 + z) < ∞ is the reciprocal of the scale
factor 0 < a ≤ 1, at high redshifts both z and (1 + z)
are very nonlinear and potentially misleading functions
of fundamental quantities such as lookback time (Sec-
tion 4.1). Had astronomers always been able to measure
accurate frequency ratios νo/νe = a instead of just small
differential wavelengths (λo −λe)/λe = z, most cosmolog-
ical equations and results would probably be presented
in terms of a today.

Notice that in W.D.Clinger's solution to v=c-Hd, both z and a are present. This actually isn't necessary. The Hubble parameter could be calculated by http://latex.codecogs.com/gif.latex?\Omega_m a^{-3}.

I think 1-r is a very interesting option.

It's between 0 and 1 for redshifts. The "r" stands for redshift, but we also use "r" for radius.

But if the radius "r" is normalized to the Hubble length, say we give it a "natural cosmological unit" where r = 1 = c/H₀, then in a de Sitter universe (and therefore in my model too) the redshift r = radius r.

 

[W.D.Clinger]

W.D.Clinger added a nice little abstraction, taking the initial distance that separates the photons out and treating it separately. So instead of two photons separated by a distance, you just have one photon and a reference distance.

That "nice little abstraction", which Mike Helland described incorrectly, was discovered by Alexander Friedmann in 1922, and is familiar to everyone who understands the FLRW models.

Notice that in W.D.Clinger's solution to v=c-Hd, both z and a are present. This actually isn't necessary. The Hubble parameter could be calculated by http://latex.codecogs.com/gif.latex?\Omega_m a^{-3}.

The highlighted sentence is absurd, as becomes apparent when the formula is checked using realistic present-day estimates of Ω_M=0.3 and a=1. H₀ is not 0.3 in any plausible units.

Mike Helland's formula could be used as a subformula of a correct computation of the Hubble parameter, but Mike Helland's formula is not by itself a correct formula for the Hubble parameter.

I am ignoring the rest of Mike Helland's most recent Gish Gallop, but the two quotations above are so far off the mark that I thought someone should mention it.

 

[Mike Helland]

That "nice little abstraction", which Mike Helland described incorrectly, was discovered by Alexander Friedmann in 1922, and is familiar to everyone who understands the FLRW models.


The highlighted sentence is absurd, as becomes apparent when the formula is checked using realistic present-day estimates of Ω_M=0.3 and a=1. H₀ is not 0.3 in any plausible units.

Mike Helland's formula could be used as a subformula of a correct computation of the Hubble parameter, but Mike Helland's formula is not by itself a correct formula for the Hubble parameter.

Huh?

Doesn't (1/(1+z))^-3 = (1+z)³

I am ignoring the rest of Mike Helland's most recent Gish Gallop, but the two quotations above are so far off the mark that I thought someone should mention it.

You don't really know what a Gish Gallop is. That's awesome.

Stay Golden, pony boy.

 

[W.D.Clinger]

Notice that in W.D.Clinger's solution to v=c-Hd, both z and a are present. This actually isn't necessary. The Hubble parameter could be calculated by http://latex.codecogs.com/gif.latex?\Omega_m a^{-3}.

The highlighted sentence is absurd, as becomes apparent when the formula is checked using realistic present-day estimates of Ω_M=0.3 and a=1. H₀ is not 0.3 in any plausible units.

Mike Helland's formula could be used as a subformula of a correct computation of the Hubble parameter, but Mike Helland's formula is not by itself a correct formula for the Hubble parameter.

Huh?

Doesn't (1/(1+z))^-3 = (1+z)³

It seems Mike Helland is now saying he believes the value of the Hubble parameter is given by (1/(1+z))^-3 = (1+z)³.

Well, let's check that. When z=0, the value of that formula is 1, which is not the value of H₀ in any plausible units.

In his two most recent posts, Mike Helland has given two distinct incorrect formulas for the Helland Hubble parameter. He didn't even notice that his two incorrect formulas yield different values for the Hubble parameter's present-day value ( H₀ ).

 

[Mike Helland]

It seems Mike Helland is now saying he believes the value of the Hubble parameter is given by (1/(1+z))^-3 = (1+z)³.

Well, let's check that. When z=0, the value of that formula is 1, which is not the value of H₀ in any plausible units.

In his two most recent posts, Mike Helland has given two distinct incorrect formulas for the Helland parameter. He didn't even notice that his two incorrect formulas yield different values for the Hubble parameter's present-day value ( H₀ ).

I only included the part of the Friedmann equation that included z.

You know that.

 

[W.D.Clinger]

I only included the part of the Friedmann equation that included z.

You know that.

The Friedmann equations don't mention z.

But Mike Helland didn't know that.

 

[Mike Helland]

The Friedmann equations don't mention z.

But Mike Helland didn't know that.

The equation I've posted a hundred times is this:

http://latex.codecogs.com/gif.latex?H = H_0 [\Omega_m (1+z)^3 + \Omega_\Lambda]^{1/2}

Whatever you call that.

 

[W.D.Clinger]

The equation I've posted a hundred times is this:

http://latex.codecogs.com/gif.latex?H = H_0 [\Omega_m (1+z)^3 + \Omega_\Lambda]^{1/2}

Whatever you call that.

I call it (Mike Helland's repetitive posting of such equations) cargo-cult physics.

Mike Helland is quite good at copy/pasting equations. He's not so good at understanding what they mean, how they're derived, or their history.

The Friedmann equations were derived in 1922 and generalized a bit in 1924.

Redshifts had been observed previously, but were attributed to the Doppler effect of what we now call peculiar motions. In 1927, Georges Lemaître used the Friedmann equations to derive the Hubble–Lemaître law, which Edwin Hubble rediscovered independently in 1929.

One of the reasons Mike Helland doesn't understand this stuff very well is that he's sort of allergic to notations that refer directly to the expansion of the universe. He prefers equations that refer to redshift z(t) over equations that refer to the scale factor a(t). He can indulge that prejudice because the two are related by (1+z)=1/a. But the scale factor a(t) is more fundamental—as a matter of history, mathematics, and physics. The redshift z(t) is a consequence of a(t), not the other way around.

But Helland physics rests upon denying that z(t) is a consequence of a(t), so Mike Helland has put a lot of effort into failing to understand the scale factor a(t) and its importance.

 

[Mike Helland]

He can indulge that prejudice because the two are related by (1+z)=1/a. But the scale factor a(t) is more fundamental—as a matter of history, mathematics, and physics. The redshift z(t) is a consequence of a(t), not the other way around.

They are both fundamentally a ratio of distances.

But Helland physics rests upon denying that z(t) is a consequence of a(t), so Mike Helland has put a lot of effort into failing to understand the scale factor a(t) and its importance.

Whatever you have to tell yourself.

 

[W.D.Clinger]

Hey folks, Mike Helland might have learned something.

Not much, but something.

He can indulge that prejudice because the two are related by (1+z)=1/a. But the scale factor a(t) is more fundamental—as a matter of history, mathematics, and physics. The redshift z(t) is a consequence of a(t), not the other way around.

They are both fundamentally a ratio of distances.

Two days ago, Mike Helland thought a(t) was just a distance:

Your algorithm still works because you've abstracted the -Hd to a reference distance "a."

As I noted at that time:

The scale factor a(t) is not a distance.

The redshift z(t) and Hubble parameter H(t) are defined in terms of the scale factor a(t).

By telling us he thinks the scale factor is a distance, Mike Helland is telling us he doesn't actually understand the definitions of redshift and the Hubble parameter.

Confirming my diagnosis, Mike Helland stated his belief that the scale factor a(t) cannot exceed unity:

Here are four ways to quantify redshift, where http://latex.codecogs.com/gif.latex?\lambda is a wavelength:

http://latex.codecogs.com/gif.latex?a = \frac{\lambda_{emit}}{\lambda_{obs}}

[...I snipped the other 3...]​

These are all fundamentally the same. The only real difference is the numeric range redshfits fall in for each.

http://latex.codecogs.com/gif.latex?0 < a < 1​

That inequality is based upon nothing more than Mike Helland's habitual focus on extrapolating backward in time instead of forward. As the universe continues to expand, the scale factor will become greater than 1.

Helland physics is based upon denying that expansion. Hence the focus. Hence his ludicrous claim that the scale factor cannot exceed 1.

But Helland physics rests upon denying that z(t) is a consequence of a(t) , so Mike Helland has put a lot of effort into failing to understand the scale factor a(t) and its importance.

Whatever you have to tell yourself.

The part I highlighted in red is a simple statement of fact.

So is the part I highlighted in blue. Mike Helland has devoted years and years of effort toward rejecting the physical relationship between z(t) and a(t).

Mike Helland could have responded by saying he now accepts that z(t) is a consequence of a(t), but that would have been an unequivocal rejection of Helland physics.

When you've worked so hard on a project for so long, it's hard to give up on it.

Easier to tell yourself a 6-word retort is clever.

 

[Mike Helland]

Two days ago, Mike Helland thought a(t) was just a distance:

False.

That inequality is based upon nothing more than Mike Helland's habitual focus on extrapolating backward in time instead of forward. As the universe continues to expand, the scale factor will become greater than 1.

Yeah, and z will be less than 0.

That's not redshift.

Helland physics is based upon denying that expansion. Hence the focus. Hence his ludicrous claim that the scale factor cannot exceed 1.

You're just making stuff up.

So is the part I highlighted in blue. Mike Helland has devoted years and years of effort toward rejecting the physical relationship between z(t) and a(t).

Uh, that's fiction. If anything I've been arguing that z isn't the best choice for quantifying redshift.

Mike Helland could have responded by saying he now accepts that z(t) is a consequence of a(t), but that would have been an unequivocal rejection of Helland physics.

You're making stuff up.

When you've worked so hard on a project for so long, it's hard to give up on it.

Easier to tell yourself a 6-word retort is clever.

Whatever you have to tell yourself.

 

[W.D.Clinger]

Two days ago, Mike Helland thought a(t) was just a distance:

False.

Mike Helland is arguing with himself.

Two days ago, he wrote this:

Your algorithm still works because you've abstracted the -Hd to a reference distance "a."

I suppose Mike Helland's understanding of the scale factor and of its role in my algorithm might have been so poor that he didn't realize the "a" in my algorithm is the scale factor (which is not a "reference distance").

That inequality is based upon nothing more than Mike Helland's habitual focus on extrapolating backward in time instead of forward. As the universe continues to expand, the scale factor will become greater than 1.

Yeah, and z will be less than 0.

That's not redshift.

As I have been saying, Mike Helland prefers talking about redshifts to talking about the scale factor a(t).

As can be seen within several of his most recent posts, Mike Helland has made the mistake of thinking a(t) is just an alternative notation for redshift.

Not so. The scale factor a(t) can (and soon will) exceed 1.

It's pretty hard to interpret a(t) > 1 as a redshift. But a(t) > 1 makes perfect sense because a(t) is a scale factor, not an alternative notation for redshift.

Mike Helland doesn't want to understand that, because Helland physics is about trying to come up with formulas that match up with redshift but don't involve expansion. That's why he likes to pretend the scale factor is just an alternative notation for redshift.

Helland physics is based upon denying that expansion. Hence the focus. Hence his ludicrous claim that the scale factor cannot exceed 1.

You're just making stuff up.

Helland physics is based upon denying the expansion of the universe. I wish I were just making that up, but I'm not. That's most of what Helland physics is about.

And that's why Mike Helland really, really doesn't want to admit the scale factor a(t) can exceed 1. If he were to admit the scale factor a(t) will exceed 1 as the universe continues to expand, he would be admitting Helland physics is rubbish.

So is the part I highlighted in blue. Mike Helland has devoted years and years of effort toward rejecting the physical relationship between z(t) and a(t).

Uh, that's fiction. If anything I've been arguing that z isn't the best choice for quantifying redshift.

I stand corrected:

Mike Helland has devoted years and years of effort toward rejecting the physical relationship between redshifts and a(t).​

Mike Helland could have responded by saying he now accepts that z(t) is a consequence of a(t), but that would have been an unequivocal rejection of Helland physics.

You're making stuff up.

What part of that could possibly be fiction?

Is Mike Helland saying it's fiction because he is psychologically incapable of responding by saying he now accepts that z(t) is a consequence of a(t)?

The only other possibility is that he's saying Helland physics is compatible with accepting that redshift is a consequence of the expanding universe. But for him to say that would itself be an unequivocal rejection of Helland physics.

'Tis a puzzlement.

 

[Mike Helland]

I suppose Mike Helland's understanding of the scale factor and of its role in my algorithm might have been so poor that he didn't realize the "a" in my algorithm is the scale factor (which is not a "reference distance").

Again, making things up for no reason.

Yes, I realized that's the scale factor. Did you realize it's also a worldline?

You algorithm sets the value of "a" at t₀ to 1.

So a₀ = 1.

Then it gets smaller. After 1 step, a₁ = a₀ - H * a₀.

The result is you're tracking the world line of an object is 1 million light years away at t=0 back to the big bang.

d(z) = a d₀

In this case d₀ = 1, so d(z) = a.

As I have been saying, Mike Helland prefers talking about redshifts to talking about the scale factor a(t).

Complete fabrication. Especially since it makes no sense to view them as conceptually unique.

Not so. The scale factor a(t) can (and soon will) exceed 1.

a(t_now) = 1, so any point in the future means a > 1.

Are you intentionally going for the spaceballs things, here?

When will then be now?

It's pretty hard to interpret a(t) > 1 as a redshift.

That's because it's blueshift.

Is everyone on this ship a Clinger?

Mike Helland doesn't want to understand that, because Helland physics is about trying to come up with formulas that match up with redshift but don't involve expansion.

Turns out my formula actually describes an expanding universe pretty well. That's the plot twist.

 

[W.D.Clinger]

Yes, I realized that's the scale factor. Did you realize it's also a worldline?

You algorithm sets the value of "a" at t₀ to 1.

So a₀ = 1.

Then it gets smaller. After 1 step, a₁ = a₀ - H * a₀.

The highlighted claim is false.

By making that claim, Mike Helland incorrectly assumed I was using a naïve Euler method with a step size of 1.

My code uses the classic Runge-Kutta method, aka RK4.

Mike Helland's mistake is not terribly important, but it's another reminder of his naïveté when it comes to algorithms and computer programming. You'd think the presence of a procedure named "runge-kutta-4" would have offered him a clue, but I guess he didn't bother to look at the code I gave him.

 

[Mike Helland]

The highlighted claim is false.

By making that claim, Mike Helland incorrectly assumed I was using a naïve Euler method with a step size of 1.

My code uses the classic Runge-Kutta method, aka RK4.

Mike Helland's mistake is not terribly important, but it's another reminder of his naïveté when it comes to algorithms and computer programming. You'd think the presence of a procedure named "runge-kutta-4" would have offered him a clue, but I guess he didn't bother to look at the code I gave him.

I'm taking about what's being integrated, and you're back to the method of integration (which is inconsequential).

 

[Mike Helland]

ETA:
The bog-standard algorithm solves the differential equation

da/dt = H(t) a(t)​

and uses that solution to drive all auxiliary calculations.

Mike Helland thinks it's better to use his ad hoc technique for updating z, in which x1−x2 serves as a proxy for the scale factor a(t).

But it isn't better. Most of the calculations we'd want to perform don't involve those particular distances x1 and x2 at all, making them extraneous. Mike Helland's algorithm has to compute x1 and x2 even when they are conceptually irrelevant to the calculation we want to perform.​

I think I've shown clearly, that in my algorithm, the change in wavelength and time dilation of light in an expanding universe are apparent in the physical magnitudes directly represented.

W.D.Clinger's variation doesn't show this directly. I think the difference is primarily pedagogical. Do you want to show (teach) redshift and time dilation as a direct consequence of the expansion of space, or do you want to show (teach) the role of the scale factor, a ratio of physical magnitudes, in FLRW?

Both would seem to have their purpose. Both take care of the issue of calculating d(t). From Sept 24 :

For any redshift, v = H(t)d(t) is accurate.

Yes, but calculating or approximating d(t) is an issue.

We've now seen it is pretty simple.

Assuming you know d₀

d(t) = a(t) d₀​

So how do we find a(t). Like this:

H0km = 68
ΩΛ = 0.7
Ωm = 0.3

H0 = H0km / 3.08e19 * 3600 * 24 * 365 * 1e6
H = H0
c = 1
t = 0
d0 = 1 
d = d0

data = [] 

while d > 0:
    t -= 1

    d -= H * d
    
    a = d / d0
    
    H = H0 * (Ωm * a**-3 + ΩΛ)**0.5    
    
    data.append([t, d])

This makes the whole world line for an object back to a big bang. You could obviously stop it in the while condition for the "t" you want.

If you were feeling extra saucy, you could substitute a**-3 for (d/d0)**-3 and you see it works just fine, skipping a and z all together. H is enough.

If you don't know d₀

Assuming we are interested in a lookback time, but we don't know the redshift, or current distance, we send a photon back in time, to see where it would be emitted from:

c = 1
t = 0
a = 1
d = 0

data = [] 

while d >= 0:
    t -= 1
    
    d += c - H * d

    a -= H * a
    
    H = H0 * (Ωm * a**-3 + ΩΛ)**0.5    
    
    data.append([t, d])

You might be wondering what this is:

    H = H0 * (Ωm * a**-3 + ΩΛ)**0.5

That's the first Friedmann equation:

https://en.wikipedia.org/wiki/Friedmann_equations#Detailed_derivation

The changing volume of the universe affects the matter density by the power of 3, but not dark energy.

What really makes this possible though is this line:

    d += c - H * d

This is just a natural consequence of special relativity and Hubble's law.

Forget the whole observers thing, we don't even need that. Say every object that interacts with light has a relative velocity of c with the light. That includes all observers then.

If every object is moving away at v=Hd, and light is coming toward us at v=c, their relative velocity is v=c+Hd. Which breaks special relativity.

Fix it by saying light travels at v=c-Hd. Then light is travels at c-Hd+Hd=c relativity to all objects.

So, I think that's about half of what I've needed to prove. I'm thankful for all the great posts here, particularly W.D.Clinger's, many of which must've taken considerable time and efforts. So thank you, W.D.​

 

[Mike Helland]

There seems to be a flaw in the standard cosmological model, in the flux-luminosity-distance relationship.

http://latex.codecogs.com/gif.latex?F = \frac{L}{4\pi r^2}​

The idea is the light coming from a distant galaxy is redshifted, and also time dilated, both of which "ding" the luminosity by a factor of (1+z) so:

http://latex.codecogs.com/gif.latex?F = \frac{L}{4\pi r^2} \frac{1}{(1+z)^2}​

We say that equals this:

http://latex.codecogs.com/gif.latex?\frac{L}{4\pi r^2} \frac{1}{(1+z)^2} = \frac{L}{4\pi d_L^2}​

http://latex.codecogs.com/gif.latex?r^2 (1+z)^2 = d_L^2​

http://latex.codecogs.com/gif.latex? d_L = r (1+z)​

Where d_L is the luminosity distance. This is a sort of hypothetical distance. I think of it like this. Imagine you're looking at a light bulb ten feet away with sunglasses on. How far away would you have to be standing to see the light bulb without sunglasses for it to appear the same brightness as with sunglasses and ten feet away?

It's basically saying, we know this light is redshifted and time dilated. Supposin' it wasn't, and it was a regular Euclidean space with steady time. How far away would the light source be in that space and time to appear as it does in ours?

So what's "r"? Seems there's a couple choices.

In the expanding universe, there is the distance between two galaxies at t_emit, the distance at t_now, and also the light travel time distance. All pictured here:

The shortest one is the angular diameter distance. This is the distance the light is emitted from, and this distance determines the size it appears on the sky.

Next is the distance the light actually traveled.

Then is farthest one, the distance the galaxy is now. Light hasn't traveled this far.

You would kind of think that the distance used as "r" in the luminosity relationship would be related to how the galaxy appears on the sky, the shortest one. At the very least, the distance the light has traveled. But actually, the farthest distance is used here, the distance the galaxy is now.

I haven't really heard of a good justification for that choice. What am I missing? It seems like the worst choice.

I would propose that both the "r" in the luminosity relationship and how the galaxy actually appears on the sky are wrong. They use the long and the short distance respectively. On one hand, farther than the light has traveled, on the other, ignoring the effects of redshift and time dilation entirely.

They should meet in the middle, and use the light travel distance. It's what happens to the light after all that should affect how its appears.

This leads to different predictions for the supernovae data, and also for angular size. To fit the angular size data requires an evolution of galaxy sizes that simply does not fit the data anymore. The best fit for both sort of looks like an exponentially expanding universe with a constant expansion rate.

One would have to accept that the amount of matter in the universe and the effects of gravity are completely ignored by the expansion of the universe. It just does it what it does. If it wants to expand, it's going to expand. A few baryons here and there don't bother it. It's like the honey badger of physical processes.

There's no initial singularity, so no inflation or anything like that. It's a pure dark energy universe, ala the cosmological constant, so that's still there though. Go, Einstein.

 

[Ziggurat]

There seems to be a flaw in the standard cosmological model, in the flux-luminosity-distance relationship.

There isn't. There's a flaw in your understanding.

You would kind of think that the distance used as "r" in the luminosity relationship would be related to how the galaxy appears on the sky, the shortest one. At the very least, the distance the light has traveled. But actually, the farthest distance is used here, the distance the galaxy is now.

I haven't really heard of a good justification for that choice. What am I missing? It seems like the worst choice.

It's the obvious and only choice.

Ignoring cosmology for a moment, why does luminosity fall off as 1/r²? Because as light travels out from a point source, you've got the same energy spread out over a larger and larger area, namely the surface of a sphere centered on the source. How does that area scale with radius? As r². You're reducing the power density by the area that this power is spread out over. That radius r happens to correspond to the distance to the source in Euclidean geometry, but the distance to the source isn't directly what controls the scaling, the surface area that the power spreads over is what produces the 1/r² scaling.

Now back to cosmology. Light is still being spread out over an ever-expanding area, the surface of a sphere. So the luminosity should still fall off as 1/r², for whatever r describes the area of the spherical surface light is propagating out from. And what r describes that surface? The current distance to the source, NOT the distance that the light traveled, or the distance at the time of emission.

I would propose that both the "r" in the luminosity relationship and how the galaxy actually appears on the sky are wrong.

It's not. You are. Because you don't really understand why luminosity has a 1/r² dependence in the first place, because you never actually bothered to study physics and learn the basics. You have no idea what you're doing.

 

[Mike Helland]

There isn't. There's a flaw in your understanding.

It's the obvious and only choice.

Ignoring cosmology for a moment, why does luminosity fall off as 1/r²? Because as light travels out from a point source, you've got the same energy spread out over a larger and larger area, namely the surface of a sphere centered on the source. How does that area scale with radius? As r². You're reducing the power density by the area that this power is spread out over. That radius r happens to correspond to the distance to the source in Euclidean geometry, but the distance to the source isn't directly what controls the scaling, the surface area that the power spreads over is what produces the 1/r² scaling.

Now back to cosmology. Light is still being spread out over an ever-expanding area, the surface of a sphere. So the luminosity should still fall off as 1/r², for whatever r describes the area of the spherical surface light is propagating out from. And what r describes that surface? The current distance to the source, NOT the distance that the light traveled, or the distance at the time of emission.

It's not. You are. Because you don't really understand why luminosity has a 1/r² dependence in the first place, because you never actually bothered to study physics and learn the basics. You have no idea what you're doing.

Well, that all makes sense, again. I already had that explained to me. Thanks for the reminder.

What about the angular size thing? Why doesn't expansion have any effect on that then?

That actually seems to be the bigger problem at the moment.

 

[Ziggurat]

What about the angular size thing? Why doesn't expansion have any effect on that then?

Why would it?

In a non-expanding space, what controls angular size of something you look at? How much of a circle centered on the observer that the object they're looking at takes up. If the object's diameter is 1/360th of the circumference of that circle, then that object takes up 1 degree of angular size for the observer. That ALSO means that the light coming from one side of the object is traveling at 1 degree different angle than light coming from the opposite side of the object.

OK, now what happens when we add in expansion? Light from each side of the object is approaching you from the same angle that it would have if space didn't expand. Uniform expansion doesn't distort path directions. So light from the left side is still approaching you at a 1 degree difference in angle compared to light from the right side. It takes longer for that light to arrive, but it still arrives coming from the same angle it started out at. So you still see light from the right side coming from 1 degree off compared to light from the left side, which means that you're still seeing a 1 degree angular size.

Or imagine it this way. Suppose that when that light was emitted, you were surrounded by a ring of galaxies, each touching edge to edge, what would happen as space expanded? Would the expansion of space open up apparent gaps in the ring? No, that wouldn't make any sense. But if the galaxies in this ring decreased their angular size, then there would need to be gaps because the number of galaxies you see can't change as a result of expansion. So the angular size of the galaxies cannot change as a result of expansion, because there's no way to introduce gaps in what you see.

You need to go back to basics and study physics from the ground up. You keep making really, really basic errors, and thinking that you're in a position to evaluate more complex issues. You aren't.

 

[Mike Helland]

Why would it?

In a non-expanding space, what controls angular size of something you look at? How much of a circle centered on the observer that the object they're looking at takes up. If the object's diameter is 1/360th of the circumference of that circle, then that object takes up 1 degree of angular size for the observer. That ALSO means that the light coming from one side of the object is traveling at 1 degree different angle than light coming from the opposite side of the object.

OK, now what happens when we add in expansion? Light from each side of the object is approaching you from the same angle that it would have if space didn't expand. Uniform expansion doesn't distort path directions. So light from the left side is still approaching you at a 1 degree difference in angle compared to light from the right side. It takes longer for that light to arrive, but it still arrives coming from the same angle it started out at. So you still see light from the right side coming from 1 degree off compared to light from the left side, which means that you're still seeing a 1 degree angular size.

Or imagine it this way. Suppose that when that light was emitted, you were surrounded by a ring of galaxies, each touching edge to edge, what would happen as space expanded? Would the expansion of space open up apparent gaps in the ring? No, that wouldn't make any sense. But if the galaxies in this ring decreased their angular size, then there would need to be gaps because the number of galaxies you see can't change as a result of expansion. So the angular size of the galaxies cannot change as a result of expansion, because there's no way to introduce gaps in what you see.

You need to go back to basics and study physics from the ground up. You keep making really, really basic errors, and thinking that you're in a position to evaluate more complex issues. You aren't.

Ok.

Let's say in Euclidean space, you have:

A
B              O
C

Imagine light from A, B, and C are all destined for O. And imagine these are straight laser shots.

It seems like if space expands between the light being emitted and received by O, that only the light from B might make it, while A and C miss their target.

It seems like A and C would intersect in front of O due to horizontally expanding space.

Space expands vertically though too. Is it the case that these directions always cancel out? Even with a dynamic expansion rate?

Part of what you're saying relies (or so it seems) on the fact that light leaves a place and is always coming toward you. All light from after the distance turnaround (so with z > 1.6 in LCDM) actually winds up farther away than it started at some point:

So why wouldn't the size of the object on the sky be imprinted from there? That makes the angular size plateau.

Here's what I'm really getting at.

A galaxy with a z=9.

* light emitted from: 3 billion light years
* light traveled: 12.9 billion years
* light source is now: 30 billion light years

So. In reality, we're saying light from a z=9 galaxy is reaching us today, and also some point 60 billion light years away, forming a shell with a diameter of 60 billion light years, and reducing its luminosity thusly.

However, it appears in the sky as exactly the same size as if it was only 3 billion light years away.

I get that's what the model says. But do you ever wonder if this is actually describing reality or not? I guess I'm asking, you do have any doubts about that, or does that all accurately describe the z=9 galaxy in reality?

 

[Ziggurat]

It seems like if space expands between the light being emitted and received by O, that only the light from B might make it, while A and C miss their target.

No. That's wrong. I can only guess as to your misconception, perhaps you are imagining expansion in only one direction and not all directions. But there is nothing special about B. The fact that it's in the middle is arbitrary, the inclusion of additional sources should illustratethat. As I said, uniform expansion doesn't distort lines. The direction between you and any other stationary object remains the same during uniform expansion. Lasers would not miss.

Part of what you're saying relies (or so it seems) on the fact that light leaves a place and is always coming toward you. All light from after the distance turnaround (so with z > 1.6 in LCDM) actually winds up farther away than it started at some point

Irrelevant. What matters for angular appearance is direction, not distance. And the direction never changes.

So. In reality, we're saying light from a z=9 galaxy is reaching us today, and also some point 60 billion light years away, forming a shell with a diameter of 60 billion light years, and reducing its luminosity thusly.

However, it appears in the sky as exactly the same size as if it was only 3 billion light years away.

Sounds like you want a unifying principle for these two seemingly different treatments. Ok, I'll give you one. We measure the diameter of the sphere at the point in time when the light hits the surface of the sphere, because that's when the diameter matters.

In the case of luminosity, the source is the center of the sphere and the observer is on the surface. We treat each source as pointlike, and consider the sphere of possible observers around it. In the case of angular appearance, the observer is at the center of the sphere at the source is on the surface, because the observer is point like but the source obviously cannot be or it would have zero angular size. The difference in which radius we use comes from the difference in when the light is on the surface of the relevant sphere.

I get that's what the model says. But do you ever wonder if this is actually describing reality or not? I guess I'm asking, you do have any doubts about that, or does that all accurately describe the z=9 galaxy in reality?

It's the only logical possibility. The only model dependence in what I described is the assumption that the expansion is uniform. Given that, it must be so.

 

[Mike Helland]

It's the only logical possibility.

I mean, there are other logical possibilities than a galaxy that looks 3 bly away is actually 30 bly away.

 

[Ziggurat]

I mean, there are other logical possibilities than a galaxy that looks 3 bly away is actually 30 bly away.

You misunderstand, as usual. Given a model of uniform expansion, there is no alternative to calculating luminosity based on current distance and angular appearance based on distance at time of emission. You didn't understand how the model makes those predictions, I explained to you how. I'm not addressing non-expansion models. Why would I?

 

[Mike Helland]

You misunderstand, as usual. Given a model of uniform expansion, there is no alternative to calculating luminosity based on current distance and angular appearance based on distance at time of emission. You didn't understand how the model makes those predictions, I explained to you how. I'm not addressing non-expansion models. Why would I?

So a z=9 galaxy, is 30 billion light years away, and appears, size-wise, as if it was 3 billion light years away.

You accept that with zero reservations? Not even the remotest hint of doubts?

 

[Mike Helland]

The direction between you and any other stationary object remains the same during uniform expansion. Lasers would not miss.

That makes sense. Plain as day in in polar coordinates.

ETA: This does require that A and C are free to expand away from B. I was thinking ABC represented a galaxy, with B as the middle.

Sounds like you want a unifying principle for these two seemingly different treatments. Ok, I'll give you one. We measure the diameter of the sphere at the point in time when the light hits the surface of the sphere, because that's when the diameter matters.

In the case of luminosity, the source is the center of the sphere and the observer is on the surface. We treat each source as pointlike, and consider the sphere of possible observers around it. In the case of angular appearance, the observer is at the center of the sphere at the source is on the surface, because the observer is point like but the source obviously cannot be or it would have zero angular size. The difference in which radius we use comes from the difference in when the light is on the surface of the relevant sphere.

It's the only logical possibility. The only model dependence in what I described is the assumption that the expansion is uniform. Given that, it must be so.

I think we can do a little better than that.

But I've been wrong about most things before.

This "shell" with the surface area with the luminosity and what not. What is that?

Well, that's just a 3D spatial slice at some time of a 4D light cone.

To make it easier to think about, subtract a dimension of space, so a 2D circle, and then add a dimension of time. At t=0 the area is 0, and as time goes it expands. A cone.

The "surface area" is now the circumference of a circle at a time slice of the cone.

If space were not expanding and light were not time dilated, it would still be a cone. Assuming the tip is at the origin, light is traveling at v=c, nothing weird happens.

In the standard model of cosmology, that's not an accurate description of the light cone. Over a change in cosmic time, the change in proper distance of a photon is v=c-Hd, at least for a photon headed toward us (as everything else is moving away at v=Hd). Photons headed away from us have to be moving at c+Hd.

In my model, it's still v=c-Hd, but the change in speed is "absorbed" by time instead of space.

Both models are in essence warping a 4D light cone, which, contains all the 3D spherical shells the propagation of the light makes over time.

So far so good?