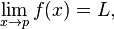Deeper than primes

[jsfisher]

'rigorous' is not less than the complementary understanding of non-locality and locality as a one unified framework.

It means that visual_spatial AND verbal_symbolic skills are actually used.

A common misunderstanding of what is written above, is based on the equivalence between 'rigorous', 'strictness', or 'step-by-step' reasoning, because only verbal_symbolic skills are used.

When I asked if you knew what the word, rigorous, meant, a simple "No" would have sufficed.

Here is an example of how 'rigour' is based only on verbal_symbolic skills ( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html ) actually does not work, exactly because by using visual_spatial AND verbal_symbolic skills epsilon > delta > 0.

Ah, Doron. I see you are back trying to disprove definitions again. The URL provides a perfectly fine definition for a certain type of limit.

Oh, and by the way, no where is it required that epsilon > delta as you claim, unless, of course, you were trying to point out yet again that when you introduce your visual/spatial skills, you get the wrong result.

 

[doronshadmi]

When I asked if you knew what the word, rigorous, meant, a simple "No" would have sufficed.

"No" is a sufficient answer only to closed systems like you that can't get http://www.internationalskeptics.com/forums/showpost.php?p=7535018&postcount=16319.

The URL provides a perfectly fine definition for a certain type of limit.


no where is it required that epsilon > delta as you claim,

This URL does not provide any "perfectly fine definition for a certain type of limit".

( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html )

The lim f(x) = L x --> a if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta.

Since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

This simple fact is easily understood by using visual_spatial AND verbal_symbolic skills.

"if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta" is based only on verbal_symbolic skills and therefore it does not hold water.

 

[jsfisher]

It does not matter

It does matter. It shows yet again how muddled your thinking is. You grossly misunderstand things then gloss over details to protect your ignorance.

both epsilon and delta > 0

Yes, that's how the definition reads, but not epsilon > delta as you alleged.

so this URL does not provide any "perfectly fine definition for a certain type of limit".

In what way is it deficient? Just because you may not like the definition, doesn't make it lacking. Mathematics is not obligated to get your approval for its terminology.

If it is deficient as a definition, surely you can provide a simple example where it comes up short.

 

[doronshadmi]

It does matter.

Yes, that's how the definition reads, but not epsilon > delta as you alleged

Again, it does not matter. What matters is that both epsilon and delta > 0.

no where is it required that epsilon > delta as you claim,

You are missing the important things (where my mistake about "epsilon > delta" does not change it (the right one is: "epsilon > 0 and delta > 0")).

This URL does not provide any "perfectly fine definition for a certain type of limit".

In what way is it deficient? Just because you may not like the definition, doesn't make it lacking. Mathematics is not obligated to get your approval for its terminology.

If it is deficient as a definition, surely you can provide a simple example where it comes up short.

( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html )

The lim f(x) = L x --> a if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta.

Since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

This simple fact is easily understood by using visual_spatial AND verbal_symbolic skills.

"if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta" is based only on verbal_symbolic skills that do not hold water, because by using these partial skills one can't understand that there is no homeomorphism between 0 dimensional space and 1 dimensional space.

It shows yet again how muddled your thinking is. You grossly misunderstand things then gloss over details to protect your ignorance.

Well, I made a mistake about "epsilon > delta" (the right one is: "epsilon > 0 and delta > 0").

This mistake does not change the fact that your verbal_symbolic_only reasoning can't comprehend that since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false, no matter what verbal_symbolic string follows it.

 

[jsfisher]

This URL does not provide any "perfectly fine definition for a certain type of limit".
...
Since |f(x) - L| > 0

You made that part up. There is no such constraint in the definition.

...and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

Again, you are trying to disprove a definition. Do you not know what a definition is?

In this particular case, the meaning of "the limit of f(x) = L as x approaches a" is being defined. That stuff between the quotes isn't true or false; it is the subject of the definition.

Definitions in Mathematics are not subject to your disapproval nor can the fall victim to disproof.

 

[doronshadmi]

You made that part up. There is no such constraint in the definition.

I know.

In order to understand that |f(x) - L| > 0 you have to use at least your visual_spatial AND verbal_symbolic skills.

Without actually doing it (which enables you to know that there is no homeomorphism between 0 dimensional space and 1 dimensional space) you can't get that the expression "f(x) = L x --> a" is false.

Again, you are trying to disprove a definition. Do you not know what a definition is?

It is a valid mathematical expression that is based at least on one's visual_spatial AND verbal_symbolic skills.

In this particular case, the meaning of "the limit of f(x) = L as x approaches a" is being defined. That stuff between the quotes isn't true or false; it is the subject of the definition.

Definitions in Mathematics are not subject to your disapproval nor can the fall victim to disproof.

"the limit of f(x) = L as x approaches a" is a false stuff.

The true stuff is "f(x) ≠ L as x approaches a" and this true stuff is known if visual_spatial AND verbal_symbolic skills are used.

 

[jsfisher]

Ok, then. Definitions are inadmissible in Doronetics. Nothing is defined.

Can't be every useful, then.

 

[jsfisher]

You made that part up. There is no such constraint in the definition.

I know

Interesting. You know it is just something you made up, but to proceed with it anyway.

In order to understand that |f(x) - L| > 0 you have to use at least your visual_spatial AND verbal_symbolic skills.

You mean your very special visual/spatial skills. The rest of us don't have your unique talent to disprove definitions by arguing against things that aren't even there.

 

[doronshadmi]

Ok, then. Definitions are inadmissible in Doronetics. Nothing is defined.

Can't be every useful, then.

A typical reply of a limited mind that is based only on verbal_symbolic skills.

 

[doronshadmi]

Interesting. You know it is just something you made up, but to proceed with it anyway.

The "I know" means that I know that you can't get what I say (you say: "There is no such constraint in the definition") because you are using only your verbal_symbolic skills.

This time please read the whole first part of http://www.internationalskeptics.com/forums/showpost.php?p=7536466&postcount=16326 in order to understand the "I know".

You mean your very special visual/spatial skills. The rest of us don't have your unique talent to disprove definitions by arguing against things that aren't even there.

Again, I know that your verbal_symbolic-only skills are insignificant in order to get that the expression "f(x) = L x --> a" is false.

Once again http://www.internationalskeptics.com/forums/showpost.php?p=7535018&postcount=16319.

 

[jsfisher]

The "I know" means that I know that you can't get what I say (you say: "There is no such constraint in the definition") because you are using only your verbal_symbolic skills.

You continue to accuse others of your own unique failings.

This time please read the whole first part of http://www.internationalskeptics.com/forums/showpost.php?p=7536466&postcount=16326 in order to understand the "I know".

Have you finally stopped revising it?

Again, I know that your verbal_symbolic-only skills are insignificant in order to get that the expression "f(x) = L x --> a" is false.

You never understood limits. We get that. That doesn't stop us from defining what we mean by an expression involving limits. If "X means Y", then I would have expected only a mentally deficient person to rant that it is not rigorous because X is false. I don't think you are mentally deficient, just a crank, but you are certainly having trouble with the whole definition concept.

 

[doronshadmi]

I don't think ...

Well, you are using partial thinking, the verbal_symbolic_only one.

This partial thinking can't actually deal with the discussed subjects, where Limit is one of them (and more generally, it can't get the actuality of Definition that is based on Visual_spatial AND Verbal_symbolic reasoning).

You never understood limits.

Wrong, your verbal_symbolic_only reasoning can't get the following valid expression "f(x) ≠ L if x only approaches (= can't actually reach) a".

Visual_spatial AND Verbal_symbolic reasoning naturally get that "f(x) ≠ L if x only approaches (= can't actually reach) a".

Some hint: There is no homeomorphism between 0 dimensional space and 1 dimensional space.

 

[jsfisher]

Wrong, your verbal_symbolic_only reasoning can't get the following valid expression "f(x) ≠ L if x only approaches (= can't actually reach) a".

First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

Third off, the whole thing is a definition. Learn to comprehend.

And as for our silly repeated gibberish about what an arbitrary function can and cannot do, consider the trivial example where f(x) = 2. Not a very interesting function, but a function nonetheless. Let L = 2, then f(x) = L as x approaches anything and everything within the domain of f().

 

[doronshadmi]

First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

Learn to understand instead of playing with symbols.

x is local w.r.t the domain of f(), where the domain of f() is non-local w.r.t x.

For example: x is equivalent to n dimensional space, where the domain of f() is equivalent to n+1 dimensional space.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, the expression "L ≠ the limit of f(x) as x approaches a" is true.

Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

"approaches" is "no more than getting closer to".

In order to "actually reach" a, x must be closest w.r.t a, such that x is actually a.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, x is "no more than getting closer to" a.

Third off, the whole thing is a definition. Learn to comprehend.

Call it whatever you like, the expression "L = the limit of f(x) as x approaches a" is a false expression.

Let L = 2, then f(x) = L as x approaches anything and everything within the domain of f().

Again, "approaches" is "no more than getting closer to" so "x approaches anything and everything within the domain of f()" means that "f(x) ≠ L".

-----------------

jsfisher, once again it is shown how your verbal_symbolic_only skills simply can't comprehend the difference between "approaches" and "actually reach", exactly because your visual_spatial skills are not used.

Once again it is shown that, for example, http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 is beyond your mind.

 

[jsfisher]

I write this:

First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

and you reply with this:

Learn to understand instead of playing with symbols.

x is local w.r.t the domain of f(), where the domain of f() is non-local w.r.t x.

For example: x is equivalent to n dimensional space, where the domain of f() is equivalent to n+1 dimensional space.

That is about as non-responsive as one can get. Doron, seriously, work on the reading comprehension.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, the expression "L ≠ the limit of f(x) as x approaches a" is true.

Hmm, now how could we possibly evaluate the merits of Doron's claim? Oh, I know, we'd need to refer to the definition of limit....

Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

"approaches" is "no more than getting closer to".

In order to "actually reach" a, x must be closest w.r.t a, such that x is actually a.

Again, learn the meaning of words. "I approach the door" does not mean "I can't reach the door." The sloppy mistakes you continue to make, Doron, are a symptom of true crank.

Third off, the whole thing is a definition. Learn to comprehend.

Call it whatever you like, the expression "L = the limit of f(x) as x approaches a" is a false expression.

Again, the only way to establish that would be to use the definition of limit. You continue to leap over that part so you can maintain your dislike for and misunderstanding of such a basic concept.

Let L = 2 [and f(x) = 2], then f(x) = L as x approaches anything and everything within the domain of f().

Again, "approaches" is "no more than getting closer to" so "x approaches anything and everything within the domain of f()" means that "f(x) ≠ L".

Excellent. According to Doron, if f(x) = 2, then f(x) ≠ 2.

You have exceeded yourself, Doron. Well done!

 

[The Man]

Indeed duality always involves both, such that it is changeable from 50%;50% which-way state (which is characterized by a wave pattern with non-strict localization) to 0%;100% which-way state (which is characterized by a single slit pattern with strict localization) by using partial measurements that are done between 50%;50% to 0%;100% , as shown, for example, in http://www.askamathematician.com/2011/06/q-what-is-a-measurement-in-quantum-mechanics/:

Doron, a single photon in impacts only a single spot on the screen. The distribution patterns you refer to are exactly that, the patterns of multiple photon impacts that are distributed over the screen. So now by your own assertions both your “non-strict localization” and “strict localization” are just distribution patterns. Would a single photon impact on the screen be a “strict localization” or a “non-strict localization”?

Dr. Shahar Dolev wrote:


I'll translate it:

"במאמר מפתח הראה אנגלרט⁵⁸ כי ניתן לגרום למערכת קוונטית לבטא את כל ספקטרום ההתנהגות שבין גל לחלקיק"

"In a Key article Englert⁵⁸ showed that it is possible to cause a quantum system to express the whole spectrum between a wave and a particle."

It does not mean that this sanctum is not a complementary state between a wave and a particle.

By using URDT one enables to measure this spectrum, which exists between the non-locality of a wave state and the locality of the particle state.

Fine then show exactly how you “measure this spectrum” with your TURD, or stop lying.

The non-locality is expressed as superposition of identities of the quantum objects, which has the symmetrical nature of wave patterns.

A gradual break of this symmetry provides the strict local nature of quantum objects as particles.

Both the 50/50 and 0/100 distribution pattern examples in the link you cited are symmetrical (though about different axis). Please learn something (like what symmetrical means).

It that your problem that you just want to conflate symmetry breaking in your nonsense somewhere?

Tools like Schrödinger equation are not useful in this case because they are based on strict variables that prevent the ability to deal with the superposition of identities of the quantum objects.

The Schrödinger equation claims no such basis, stop lying Doron.


And while you’re at it read your own cited references.

The Copenhagen interpretation of quantum mechanics (which comes in a couple different flavors) is generally stated as “a thing is in a super-position of states until it’s measured”. Some people (including very few physicists) have come to the conclusion that “measurement” means “measured by something conscious, and also we’re all part of the same energy field, so we’re psychic, and modern science is only now coming to understand what eastern philosophers have known for millennia”.

Just to be clear, the Copenhagen interpretation is a bottomless font of problems and paradoxes, of which the “measurement problem” is one of the more interesting (but still: one of many). Luckily, since Copenhagen is based on an assumption (“things are in many states until measured”) that never needed to be made, isn’t well-defined, and is in no way supported by any kind of evidence, it can be abandoned giving rise to the Many Worlds Interpretation. Sorrowfully, it’s often found unabandoned (particularly in new age literature).

He is specifically asserting the notion you cling to and so readily misrepresent (“things are in many states until measured”) should be abandoned. How’s that coming for you?

Again "A,B"-only reasoning can't comprehend, for example, http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 .

Again stop simply trying to posit aspects of your own failed reasoning onto others and indicate that specific “transition” in your TURD, as asked before.

You can't because you are closed under it.

It is just your nonsense Doron. Please show how you use it to solve anything.

First please get out of your strict-only box. Without actually doing it, you can't get URDT.

It is your “strict-only box”, simply trying to posit it onto others will not help you. You claimed a distinction with your TURD so you show that distinction with your TURD.

 

[doronshadmi]

I write this:



and you reply with this:


That is about as non-responsive as one can get. Doron, seriously, work on the reading comprehension.

jsfisher, seriously, work on getting out of your verbal_symbolic_only skills, by simply use your visual_spatial AND verbal_symbolic skills.

Hmm, now how could we possibly evaluate the merits of Doron's claim? Oh, I know, we'd need to refer to the definition of limit....

Your definition of limit is closed under your verbal_symbolic_only skills.

Again, learn the meaning of words. "I approach the door" does not mean "I can't reach the door." The sloppy mistakes you continue to make, Doron, are a symptom of true crank.

You are truly closed under your verbal_symbolic_only skills, which naturally prevents from you to distinguish between "I approach the door" and "I actually reach the door."

Again, the only way to establish that would be to use the definition of limit. You continue to leap over that part so you can maintain your dislike for and misunderstanding of such a basic concept.

Basic concepts of the considered subject can't be archived by using verbal_symbolic_only skills.

Excellent. According to Doron, if f(x) = 2, then f(x) ≠ 2.

You have exceeded yourself, Doron. Well done!

Not even closer.

"If L=2, then f(x) ≠ L as x approaches a".

This true expression is easily known if one's visual_spatial AND verbal_symbolic skills are used, which is definitely not your case, jsfisher.

For example, here is actually the same subject, which your verbal_symbolic_only skills can't actually reach:

-----------------------------------------------------------
Here is the abstract taken from Philip J. Davis and James A. Anderson book called “Nonanalytic Aspects of Mathematics and Their Implication for Research and Education,” SIAM Review 21(1979), 112-117:

Abstract
In this paper we make a distinction between the practice of mathematics as it is usually presented--a logical chain of abstract, analytical reasoning from premises to conclusions--and how mathematics seems to be done in actuality--as a series of nonverbal, analog, often kinesthetic or visual insights. Mathematics in recent years has created a hierarchy with highly abstract, logical and symbolic material at the peak and with more geometrical, visual, and analog material held to be of lesser worth. We argue that humans are known to vary widely in their approaches to cognition and that the areas of the human brain specifically related to language and logical analysis seem to comprise only a part of the machinery of our intellect. We suggest that it would be wise for the practitioners of mathematics, and perhaps especially the students of mathematics to be aware of the very important nonverbal elements in mathematics. We feel that excessive emphasis on the abstract, analytic aspects of thought may have had deleterious effects on the profession and that a more appropriate balance, more in line with our cognitive endowment as humans, is desirable.
----------------------------------------------------------

The Real-line and non-local numbers

By using verbal_symbolic AND visual_spatial skills we get a one comprehensive framework.

For example, by Traditional Mathematics (which is mostly based on verbal_symbolic skills) 0.111...₂ = 0.999...₁₀ = 1 where 1 is the considered mathematical object (the number itself) and 0.111...₂ or 0.999...₁₀ are some numerals (out of many representations) that represent number 1.

By using verbal_symbolic and visual_spatial skills as follows:

[qimg]http://farm7.static.flickr.com/6142/5962015728_d2fe37cc5f_z.jpg[/qimg]

one understands that no branch of that tree actually reaches any other branch of that tree "downward" , no matter how many levels
that tree has (in other words, there is no homeomorphism between 0 dimensional space (notated by "0";"1" symbols)
and 1 dimensional space (notated by "_____" spatial non-composed object)).

According to this comprehensive framework 0.111...₂ is a number of its own < number 1 by 0.000...1₂ where the "...1" part
of that number is the irreducibility of ___ 1 dimensional space into 0 dimensional space (known as a point).

By using verbal_symbolic and visual_spatial skills one enables to distinguish between non-local numbers like 0.111...₂ or 0.000...1₂, and local numbers like 1.

Furthermore, no collection of, for example, 0 dimensional spaces along a 1 dimensional space has the power of the continuum of a 1 dimensional space.

By understanding the power of the continuum in terms of spatial skills, one understands that no collection of sub-objects of a given space (mathematical or physical) has the power of the continuum of that space, or in other words, any given collection of sub-objects is incomplete with respect to the "host" space.

The non-locality of 0.111...₂ or 0.000...1₂ is "naturally vague" in terms of location, and one actually discovers/invents that the Real-line has a non-empty set of non-strict numbers between 0 dimensional space and 1 dimensional space.

(By generalization, given a "host" space, no collection of "hosted" spaces has the power of the "host" space).

----------------------------------------------------------

 

[doronshadmi]

Doron, a single photon in impacts only a single spot on the screen.

Because the screen destroys the superposition of identities of the quantum objects.

Would a single photon impact on the screen be a “strict localization” or a “non-strict localization”?

Only “strict localization” because the screen destroys the superposition of identities of the quantum objects.

The distribution patterns you refer to are exactly that, the patterns of multiple photon impacts that are distributed over the screen. So now by your own assertions both your “non-strict localization” and “strict localization” are just distribution patterns.

The distribution patterns of "strict spots" is exactly the signature of the interaction among quantum objects, before they hit the screen and collapse into "strict spots". The distribution of wave patterns actually manifests the superposition of identities of the quantum objects before they hit the screen, where the distribution of a single peak pattern manifests the strict identities of the quantum objects before they hit the screen.

After all quantum objects are wavicles even if their wave properties and particle properties can't be manifested simultaneously.

Fine then show exactly how you “measure this spectrum” with your TURD, or stop lying.

TURD is your ill attitude of URDT, which is characterized by your "closed box" syndrome about this fine subject . As long as this is your initial attitude there is no use to talk with you about URDT.

Can you change your attitude about this fine subject?

The non-locality is expressed as superposition of identities of the quantum objects, which has the symmetrical nature of wave patterns.

A gradual break of this symmetry provides the strict local nature of quantum objects as particles.

Both the 50/50 and 0/100 distribution pattern examples in the link you cited are symmetrical (though about different axis). Please learn something (like what symmetrical means).

The Man, you defiantly have no clue about the symmetry of superposition of identities, because you do not distinguish, for example, between "AB" (which is an example of the symmetry among superposition of identities) and "A,B" (which is an example of the asymmetry among strict identities), exactly because your reasoning is closed under "A,B".

It that your problem that you just want to conflate symmetry breaking in your nonsense somewhere?

It that your problem that you just want to conflate symmetry by using your asymmetric "A,B"-only view?

The Schrödinger equation claims no such basis, stop lying Doron.

Once again, it can't claim such basis, exactly because it is the expression of "A,B"-only reasoning.

(“things are in many states until measured”)

It is not less than the symmetry of superposition of identities.

You can't comprehend that as long as you are closed under your asymmetric "A,B"-only reasoning.

The Man, you actually doing your best in order to stay closed under your asymmetric "A,B"-only reasoning all along this thread.

 

[doronshadmi]

Approach vs. reach:

http://www.usingenglish.com/forum/ask-teacher/27922-approach-vs-reach.html


Approach:

http://www.merriam-webster.com/dictionary/approach

http://dictionary.reference.com/browse/approach

http://en.wiktionary.org/wiki/approach


Reach:

http://dictionary.reference.com/browse/reach

http://www.thefreedictionary.com/reach

http://www.merriam-webster.com/dictionary/reach?show=0&t=1315216231


----------------------


http://en.wikipedia.org/wiki/Limit_of_a_function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input.

Informally, a function f assigns an output f(x) to every input x. The function has a limit L at an input p if f(x) is "close" to L whenever x is "close" to p. In other words, f(x) becomes closer and closer to L as x moves closer and closer to p. More specifically, when f is applied to each input sufficiently close to p, the result is an output value that is arbitrarily close to L.

To say that

means that ƒ(x) can be made as close as desired to L by making x close enough, but not equal, to p.

----------------------

In other words, jsfisher's community (which is based on verbal_symbolic_only skills) is wrong, formally and informally,
exactly because ƒ(x) ≠ L since x ≠ p.

 

[jsfisher]

Approach vs. reach:
...
Approach:
...
Reach:

Doron, it doesn't matter one twit what you think the word, approach, should or should not mean in the limit definition. The fact remains, the definition itself tells us exactly what is meant by it.

Stop trying to disprove definitions. It cannot be done.