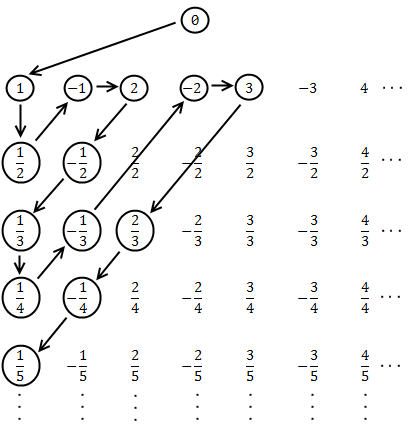
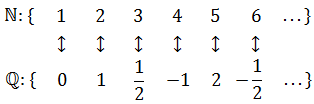HatRack, if you are non-constructivist you do not need any index to assume that there is a set of all infinitely many distinct irrational members.
Wow Doron, you are so confused about something so simple. Being a non-constructivist does not mean that you can assume the existence of whatever you like. It means that you do not have to explicitly construct something to show that it exists.
I am perfectly fine with proofs of the form "Assume A doesn't exist -> Proposition -> Proposition -> ... -> Contradiction -> Therefore A exists", and so I am a non-constructivist. That's all it means, stop reinventing terminology that you don't understand.
That being said, the fact that the set of irrational numbers exists and is infinite is true, but it follows from more basic assumptions, it is not an assumption itself. The problem is that you cannot construct a sequence of irrational numbers without using the natural numbers implicitly as indexes.
If you don't understand sequences in mathematics and how they are defined rigorously, then you cannot possibly comprehend what Cantor's Diagonal Argument is really saying.
By using the diagonal method it is proved that such a set is incomplete (the set of all irrational numbers does not exist).
Nonsense. No one has shown any such thing. Cantor's diagonal argument starts out with the assumption that a bijection between the natural numbers and the interval (0,1) exists. Nothing can be concluded with a proof that starts out with "Assume A" unless you reach a contradiction, at which point you can conclude "Not A". This is exactly the form of Cantor's Diagonal Argument, and the fact that you try to conclude something that is in no way related to the original proposition A is just plain dumb and wrong.
Last edited: