We have already established that a z=9 galaxy spreads out its light over a surface area of 4pi(30 Gly)
2 in just 12.9 billion years (in LCDM).
If that's true the light's change in position over a change in time had to have exceeded c.
If that's just a map, if that's not "real" then the expansion of space is an illusion and there was no big bang.
As to the map-territory platitude...
Which territory are speaking about now? The manifold? Or the ambient space?
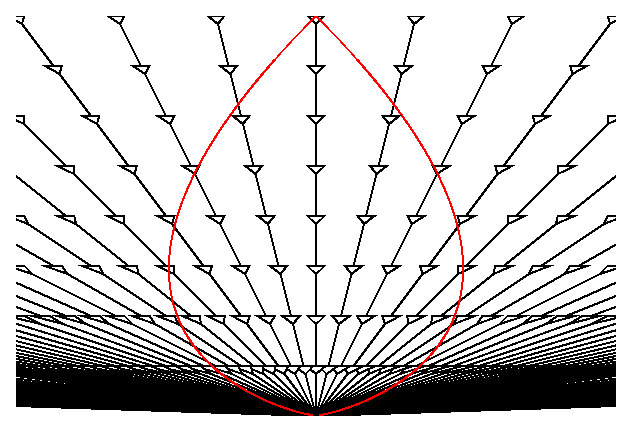
Our three dimensions of space and one dimension of time exist on the surface of a 5D shape in a 5D space called ambient space.
In the ambient space, dimensions are invariant and the speed of light is always c.
The null paths on the manifold are described by the interaction of the manifold with another shape, the light cone.
[qimg]http://www.internationalskeptics.com/forums/imagehosting/thum_762186543cb01b1a33.png[/qimg]
FLRW is basically a clever hack to change the speed of light.
After every second that light has traveled, spacetime says "ok, good, this next second, you're going to have to travel a little bit farther."
My metric is a less clever hack to mimic FLRW, but by changing clock rates instead distances.
Both are obtuse and lead to singularities, just in different places. Both begin, unjustifiably, with invariant space, time, and speed of light in ambient space. It's all neat-o math stuff, but the 5D is clearly removed from our reality.
Here's what the metric itself says.
http://latex.codecogs.com/gif.latex?ds^2 = -c^2 dt^2 + a(t)^2 dx^2
http://latex.codecogs.com/gif.latex?0 = -c^2 dt^2 + a(t)^2 dx^2
http://latex.codecogs.com/gif.latex?c^2 dt^2 = a(t)^2 dx^2
http://latex.codecogs.com/gif.latex?c^2 = a(t)^2 \frac{dx^2}{dt^2}
http://latex.codecogs.com/gif.latex?\frac{c^2}{a(t)^2} = \frac{dx^2}{dt^2}
http://latex.codecogs.com/gif.latex?\frac{dx}{dt} = \frac{c}{a(t)}